[题目]某位股民购进某只股票.在接下来的交易时间内.他的这只股票先经历了次涨停(每次上涨 ).又经历了次跌停(每次下跌 ).则该股民这只股票的盈亏情况A.略有盈利B.略有亏损C.没有盈利也没有亏损D.无法判断盈亏情况题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某位股民购进某只股票，在接下来的交易时间内，他的这只股票先经历了次涨停（每次上涨），又经历了次跌停（每次下跌），则该股民这只股票的盈亏情况（不考虑其他费用）是（）
A.略有盈利
B.略有亏损
C.没有盈利也没有亏损
D.无法判断盈亏情况

【答案】B
【解析】设这只票购进价格为，则这只股票先经历了n次涨停(每次上涨10%)，又经历了n次跌停(每次下跌10%)后的价格为：，所以该股民这只股票略有亏损．所以答案是：B．

【考点精析】通过灵活运用用样本的数字特征估计总体的数字特征，掌握用样本估计总体时，如果抽样的方法比较合理，那么样本可以反映总体的信息，但从样本得到的信息会有偏差．在随机抽样中，这种偏差是不可避免的即可以解答此题．

练习册系列答案

品至教育假期复习计划期末寒假衔接系列答案

假期园地寒假系列答案

假期生活寒假花山文艺出版社系列答案

南方凤凰台假期之友寒假作业江苏凤凰教育出版社系列答案

假期总动员寒假最佳学习方案系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且cos2B+3cos（A+C）+2=0，，那么△ABC周长的最大值是（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）与g（x）的图象关于原点对称，且它们的图象拼成如图所示的“Z”形折线段ABOCD，不含A（0，1），B（1，1），O（0，0），C（﹣1，﹣1），D（0，﹣1）五个点．则满足题意的函数f（x）的一个解析式为．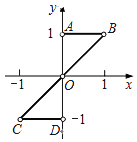

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某景点拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为36米，其中大圆弧所在圆的半径为14米，设小圆弧所在圆的半径为x米，圆心角为θ（弧度）．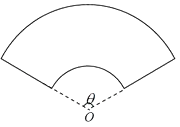

（1）求θ关于x的函数关系式；
（2）已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为16元/米，设花坛的面积与装饰总费用之比为y，求y关于x的函数关系式，并求出y的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知命题P：函数的定义域为R；命题q：x∈R，使不等式a＞e2x﹣ex成立；命题“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于数列，，，，若满足，则称数列为“ 数列”．
若存在一个正整数，若数列中存在连续的项和该数列中另一个连续的项恰好按次序对应相等，则称数列是“ 阶可重复数列”，
例如数列因为，，，与，，，按次序对应相等，所以数列是“ 阶可重复数列”．
（I）分别判断下列数列，，，，，，，，，．是否是“ 阶可重复数列”？如果是，请写出重复的这项；
（II）若项数为的数列一定是 “ 阶可重复数列”，则的最小值是多少？说明理由；
（III）假设数列不是“ 阶可重复数列”，若在其最后一项后再添加一项或，均可使新数列是“ 阶可重复数列”，且，求数列的最后一项的值．