
【题目】已知函数f(x)=lnx﹣x, ![]() .
.
(1)求h(x)的最大值;
(2)若关于x的不等式xf(x)≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,求实数a的取值范围;
(3)若关于x的方程f(x)﹣x3+2ex2﹣bx=0恰有一解,其中e是自然对数的底数,求实数b的值.
【答案】
(1)解:因为 ![]() ,所以
,所以 ![]() ,
,
由h′(x)>0,且x>0,得0<x<e,由h′(x)<0,且x>0,x>e,
所以函数h(x)的单调增区间是(0,e],单调减区间是[e,+∞),
所以当x=e时,h(x)取得最大值 ![]() ;
;
(2)因为xf(x)≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,
即xlnx﹣x2≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,
亦即 ![]() 对一切x∈(0,+∞)恒成立,
对一切x∈(0,+∞)恒成立,
设 ![]() ,因为
,因为 ![]() ,
,
故(x)在(0,3]上递减,在[3,+∞)上递增,(x)min=(3)=7+ln3,
所以a≤7+ln3.
(3)因为方程f(x)﹣x3+2ex2﹣bx=0恰有一解,
即lnx﹣x﹣x3+2ex2﹣bx=0恰有一解,即 ![]() 恰有一解,
恰有一解,
由(1)知,h(x)在x=e时, ![]() ,
,
而函数k(x)=x2﹣2ex+b+1在(0,e]上单调递减,在[e,+∞)上单调递增,
故x=e时,k(x)min=b+1﹣e2,
故方程 ![]() =x2﹣2ex+b+1恰有一解当且仅当b+1﹣e2=
=x2﹣2ex+b+1恰有一解当且仅当b+1﹣e2= ![]() ,
,
即b=e2+ ![]() ﹣1;
﹣1;
【解析】1、由h′(x)>0,且x>0,得0<x<e,由h′(x)<0,且x>0,x>e,所以函数h(x)的单调增区间是(0,e],单调减区间是[e,+∞)所以当x=e时,h(x)取得最大值 ![]() .
.
2、因为xf(x)≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,亦即 a ≤ l n x + x + ![]() 对一切x∈(0,+∞)恒成立.设 ( x ) = l n x + x +
对一切x∈(0,+∞)恒成立.设 ( x ) = l n x + x + ![]() ,求导可得,(x)在(0,3]上递减,在[3,+∞)上递增,(x)min=(3)=7+ln3,所以a≤7+ln3.
,求导可得,(x)在(0,3]上递减,在[3,+∞)上递增,(x)min=(3)=7+ln3,所以a≤7+ln3.
【考点精析】掌握利用导数研究函数的单调性和函数的零点是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.
在这个区间单调递减;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某景点拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为36米,其中大圆弧所在圆的半径为14米,设小圆弧所在圆的半径为x米,圆心角为θ(弧度).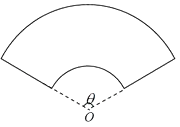
(1)求θ关于x的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为16元/米,设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若满足
,若满足 ![]() ,则称数列
,则称数列 ![]() 为“
为“ ![]() 数列”.
数列”.
若存在一个正整数 ![]() ,若数列
,若数列 ![]() 中存在连续的
中存在连续的 ![]() 项和该数列中另一个连续的
项和该数列中另一个连续的 ![]() 项恰好按次序对应相等,则称数列
项恰好按次序对应相等,则称数列 ![]() 是“
是“ ![]() 阶可重复数列”,
阶可重复数列”,
例如数列 ![]() 因为
因为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,所以数列
按次序对应相等,所以数列 ![]() 是“
是“ ![]() 阶可重复数列”.
阶可重复数列”.
(I)分别判断下列数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .是否是“
.是否是“ ![]() 阶可重复数列”?如果是,请写出重复的这
阶可重复数列”?如果是,请写出重复的这 ![]() 项;
项;
(II)若项数为 ![]() 的数列
的数列 ![]() 一定是 “
一定是 “ ![]() 阶可重复数列”,则
阶可重复数列”,则 ![]() 的最小值是多少?说明理由;
的最小值是多少?说明理由;
(III)假设数列 ![]() 不是“
不是“ ![]() 阶可重复数列”,若在其最后一项
阶可重复数列”,若在其最后一项 ![]() 后再添加一项
后再添加一项 ![]() 或
或 ![]() ,均可 使新数列是“
,均可 使新数列是“ ![]() 阶可重复数列”,且
阶可重复数列”,且 ![]() ,求数列
,求数列 ![]() 的最后一项
的最后一项 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求∠C;
(2)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长;
,求△ABC的周长;
(3)若c= ![]() ,求△ABC的周长的取值范围.
,求△ABC的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王先生家住 A 小区,他工作在 B 科技园区,从家开车到公司上班路上有 L1 , L2两条路线(如图),L1路线上有 A1 , A2 , A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有 B1 , B2两个路.各路口遇到红灯的概率依次为
;L2路线上有 B1 , B2两个路.各路口遇到红灯的概率依次为 ![]() ,
, ![]() .若走 L1路线,王先生最多遇到 1 次红灯的概率为;若走 L2路线,王先生遇到红灯次数 X 的数学期望为 .
.若走 L1路线,王先生最多遇到 1 次红灯的概率为;若走 L2路线,王先生遇到红灯次数 X 的数学期望为 . 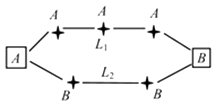
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x0 , y0)在x2+y2=r2(r>0)外,则直线x0x+y0y=r2与圆x2+y2=r2的位置关系为( )
A.相交
B.相切
C.相离
D.相交、相切、相离三种情况均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com