
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 27 |
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 27 |
| 2 |
| 3 |
2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 20 |
| 27 |
| X | 3 | 5 | ||||
| P |
|
|
| 7 |
| 27 |
| 20 |
| 27 |
| 121 |
| 27 |


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
| y0 |
| x0 |
A、(-
| ||||
B、[-
| ||||
C、(-
| ||||
D、(-∞,-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男性 | 5 | ||
| 女性 | 10 | ||
| 合计 | 50 |
| 4 |
| 49 |
| P(K2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| Sn |
| n |
| 1 |
| 2 |
| 11 |
| 2 |
| 3 |
| (2an-11)(2bn-1) |
| k |
| 57 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
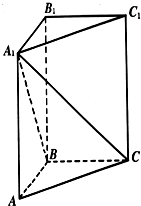 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com