
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=  .
.
(1)求年利润W(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大值.
【答案】
(1)解:当0<x≤10时,
W=xR(x)﹣(10+2.7x)=8.1x﹣ ![]() ﹣10,
﹣10,
当x>10时,W=xR(x)﹣(10+2.7x)=98﹣ ![]() ﹣2.7x,
﹣2.7x,
∴W= 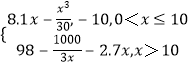 .
.
(2)解:①当0<x≤10时,
由W′=8.1﹣ ![]() =0,得x=9,且当x∈(0,9)时,w′>0,
=0,得x=9,且当x∈(0,9)时,w′>0,
当x∈(9,10)时,w′<0.
∴当x=9时,W取最大值,且wmax=8.1×9﹣ ![]() ﹣10=38.6
﹣10=38.6
x>10时,W=98﹣( ![]() )≤98﹣2
)≤98﹣2 ![]() =38,
=38,
当且仅当 ![]() =2.7x,即x=
=2.7x,即x= ![]() 时W取得最大值38.
时W取得最大值38.
综合①②知:当x=9时,W取得最大值38.6.故当年产量为9千件时,该公司在这一品牌服装的生产中所获的年利润最大.
【解析】(1)当0<x≤10时,W=xR(x)﹣(10+2.7x)=8.1x﹣ ![]() ﹣10,当x>10时,W=xR(x)﹣(10+2.7x)=98﹣
﹣10,当x>10时,W=xR(x)﹣(10+2.7x)=98﹣ ![]() ﹣2.7x,由此能求出年利润W(万元)关于该特许商品x(千件)的函数解析式.(2)当0<x≤10时,由W′=8.1﹣
﹣2.7x,由此能求出年利润W(万元)关于该特许商品x(千件)的函数解析式.(2)当0<x≤10时,由W′=8.1﹣ ![]() =0,得x=9,推导出当x=9时,W取最大值,且wmax=38.6;当x>10时,W≤38.由此得到当年产量为9千件时,该公司在该特许商品生产中获利最大.
=0,得x=9,推导出当x=9时,W取最大值,且wmax=38.6;当x>10时,W≤38.由此得到当年产量为9千件时,该公司在该特许商品生产中获利最大.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若不过原点的直线l与圆C相切,且在x轴,y轴上的截距相等,求直线l的方程;
(2)从圆C外一点P(x,y)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人们生活水平的提高,越来越注重科学饮食.营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪.1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,每天需要同时食用食物A和食物B多少kg?最低花费是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b是两个实数,给出下列条件:
①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1.
其中能推出:“a,b中至少有一个大于1”的条件是 .(填序号,只有一个正确选项)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0;
②f( ![]() )=1;
)=1;
③对任意的正实数x,y,都有f(xy)=f(x)+f(y).
(1)求证:f( ![]() )=﹣f(x);
)=﹣f(x);
(2)求证:f(x)在定义域内为减函数;
(3)求满足不等式f(log0.5m+3)+f(2log0.5m﹣1)≥﹣2的m集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ![]() ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+ ![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 ![]() >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+2x+x﹣1,若f(x2﹣4)<2,则实数x的取值范围是( )
A.(﹣2,2)
B.(2, ![]() )
)
C.(﹣ ![]() ,﹣2)
,﹣2)
D.(﹣ ![]() ,﹣2)∪(2,
,﹣2)∪(2, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com