
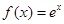 ,
, .
. 时,证明:
时,证明: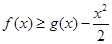 ;
;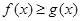 ,求k的取值范围.
,求k的取值范围.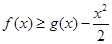 转化为
转化为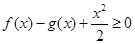 ,先得到
,先得到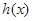 表达式,对
表达式,对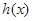 求导,利用“
求导,利用“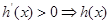 单调递增;
单调递增;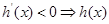 单调递减”解不等式求函数
单调递减”解不等式求函数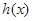 的单调区间,利用函数的单调性确定最小值所在的位置;第二问,将
的单调区间,利用函数的单调性确定最小值所在的位置;第二问,将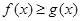 转化为
转化为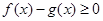 ,令F(x)=f(x)-g(x)对f(x)求导,由于
,令F(x)=f(x)-g(x)对f(x)求导,由于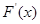 的正负不明显,所以进行二次求导,二次求导后得到G¢(x)=ex-k,只需讨论k的正负,通过
的正负不明显,所以进行二次求导,二次求导后得到G¢(x)=ex-k,只需讨论k的正负,通过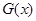 的单调性,求出
的单调性,求出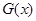 的最值,来判断
的最值,来判断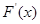 的正负,来判断
的正负,来判断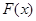 的单调性,从而求
的单调性,从而求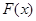 的最值.
的最值.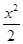 =ex-x-1,h¢(x)=ex-1. 1分
=ex-x-1,h¢(x)=ex-1. 1分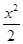 . 4分
. 4分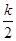 x2-x-1,则F¢(x)=ex-kx-1.
x2-x-1,则F¢(x)=ex-kx-1.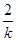 )时,ex-1<0,-
)时,ex-1<0,-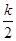 x2-x=-
x2-x=-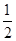 x(kx+2)<0,
x(kx+2)<0,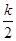 x2-x<0,这时f(x)≥g(x)不成立. 11分
x2-x<0,这时f(x)≥g(x)不成立. 11分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com