
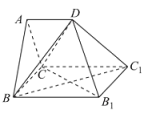
【题目】如图,多面体![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 为原正三棱柱的底面,
为原正三棱柱的底面,![]() ,点D为
,点D为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() ,由题意可得四边形
,由题意可得四边形![]() 是正方形,且
是正方形,且![]() ,再由点D为
,再由点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,求得CD,同理求得
,求得CD,同理求得![]() ,得
,得![]() ,可得
,可得![]() ,由线面垂直的判定可得;
,由线面垂直的判定可得;
(2)取BC的中点O,连接AO,可得AO⊥BC,由正棱柱的性质可得AO⊥平面![]() ,以O为坐标原点,向量
,以O为坐标原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面
分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面![]() 的一个法向量,由两法向量所成角的余弦值可得二面角
的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() .
.
∵多面体![]() 是正三棱柱沿平面
是正三棱柱沿平面![]() 切除部分所得,
切除部分所得,![]() ,
,
∴四边形![]() 是正方形,且
是正方形,且![]() .
.
∵点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,
,
∴![]() .
.
同理![]() ,
,
∴![]() .
.
∵E为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)取![]() 的中点O,连接
的中点O,连接![]() .
.
∵![]() 为正三角形,
为正三角形,![]() .
.
由正棱柱的性质可得,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
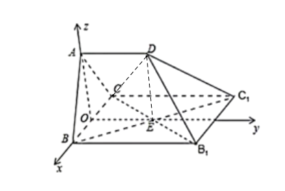
以点O为原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴正方向建立如图所示空间直角坐标系
分别为x、y,z轴正方向建立如图所示空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则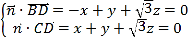 ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
由(1)可知,平面![]() 的一个法向量为
的一个法向量为![]() .
.
 ,
,
又∵二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】对于数列![]() ,定义“
,定义“![]() 变换”:
变换”:![]() 将数列
将数列![]() 变换成数列
变换成数列![]() ,其中
,其中![]() ,且
,且![]() ,这种“
,这种“![]() 变换”记作
变换”记作![]() .继续对数列
.继续对数列![]() 进行“
进行“![]() 变换”,得到数列
变换”,得到数列![]() ,依此类推,当得到的数列各项均为
,依此类推,当得到的数列各项均为![]() 时变换结束.
时变换结束.
(1)试问![]() 和
和![]() 经过不断的“
经过不断的“![]() 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“![]() 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;
(2)求![]() 经过有限次“
经过有限次“![]() 变换”后能够结束的充要条件;
变换”后能够结束的充要条件;
(3)证明:![]() 一定能经过有限次“
一定能经过有限次“![]() 变换”后结束.
变换”后结束.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A.若命题![]() 为真命题,命题
为真命题,命题![]() 为假命题,则命题“
为假命题,则命题“![]() ”为真命题
”为真命题
B.命题“若![]() ,则
,则![]() 或
或![]() ”为真命题
”为真命题
C.命题“若![]() ,则
,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() 且
且![]() ”
”
D.命题![]() :
:![]() ,
,![]() ,则
,则![]() 为
为![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆E:![]() 的左、右焦点,且|F1F2|=2
的左、右焦点,且|F1F2|=2![]() ,点
,点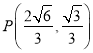 在E上.
在E上.
(1)求E的方程;
(2)直线l与以E的短轴为直径的圆相切,l与E交于A,B两点,O为坐标原点,试判断O与以AB为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴建立极坐标系,则曲线
轴非负半轴为极轴建立极坐标系,则曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程与
的普通方程与![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 是曲线
是曲线![]() 上一点,由
上一点,由![]() 向圆
向圆![]() 引切线,切点分别为
引切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]()
![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市管辖的海域内有一圆形离岸小岛,半径为1公里,小岛中心O到岸边AM的最近距离OA为2公里.该市规划开发小岛为旅游景区,拟在圆形小岛区域边界上某点B处新建一个浴场,在海岸上某点C处新建一家五星级酒店,在A处新建一个码头,且使得AB与AC满足垂直且相等,为方便游客,再建一条跨海高速通道OC连接酒店和小岛,设![]() .
.
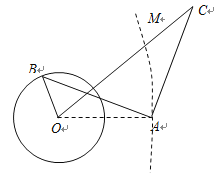
(1)设![]() ,试将
,试将![]() 表示成
表示成![]() 的函数;
的函数;
(2)若OC越长,景区的辐射功能越强,问当![]() 为何值时OC最长,并求出该最大值.
为何值时OC最长,并求出该最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com