
【题目】设函数![]() .
.
(1)讨论函数![]() 的极值;
的极值;
(2)若![]() 为整数,
为整数,![]() ,且
,且![]() ,不等式
,不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,
时,![]() 有极大值
有极大值![]() ,无极小值;(2)2
,无极小值;(2)2
【解析】
(1)先对函数求导,得到![]() ,分别讨论
,分别讨论![]() 与
与![]() 两种情况,用导数的方法研究函数单调性,即可求出结果;
两种情况,用导数的方法研究函数单调性,即可求出结果;
(2)先由![]() ,将不等式
,将不等式![]() 化为
化为![]() ,进而将问题转化为
,进而将问题转化为![]()
![]() 恒成立;令
恒成立;令![]() ,
,![]() ,用导数的方法研究其单调性,求出最值,即可得出结果.
,用导数的方法研究其单调性,求出最值,即可得出结果.
(1)因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() 恒成立,因此
恒成立,因此![]() 在
在![]() 上单调递减,此时无极值;
上单调递减,此时无极值;
当![]() 时,由
时,由![]() 得
得![]() ;由
;由![]() 得
得![]() ;
;
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
因此![]() 有极大值
有极大值![]() ;
;
综上所示,当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,
时,![]() 有极大值
有极大值![]() ,无极小值;
,无极小值;
(2)当![]() 时,
时,![]() ,
,
所以不等式![]() 可化为
可化为![]() ,
,
因此![]() ,不等式
,不等式![]() 成立,可化为
成立,可化为![]()
![]() 恒成立;
恒成立;
令![]() ,
,![]() ,
,
则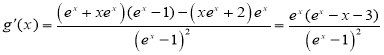 ,
,
令![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() ,即
,即![]() ;
;
所以当![]() 时,
时,![]() ,即
,即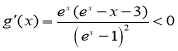 ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,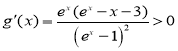 ,
,![]() 单调递增;
单调递增;
所以![]() ,
,
因此只需![]() ,即
,即![]() 的最大值为
的最大值为![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数,则下列结论中错误的个数是( )
的导函数,则下列结论中错误的个数是( )
①函数![]() 的值域与
的值域与![]() 的值域相同;
的值域相同;
②若![]() 是函数
是函数![]() 的极值点,则
的极值点,则![]() 是函数
是函数![]() 的零点;
的零点;
③把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,就可以得到
个单位长度,就可以得到![]() 的图像;
的图像;
④函数![]() 和
和![]() 在区间
在区间![]() 内都是增函数.
内都是增函数.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数具有性质
,则称函数具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并证明:①
,并证明:①![]() (
(![]() );②
);②![]() ;
;
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() (
(![]() ,
,![]() ),
),
①求证:对任意![]() ,有
,有![]() ;
;
②是否对任意![]() ,均有
,均有![]() ?若有,给出证明,若没有,给出反例.
?若有,给出证明,若没有,给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究.该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).
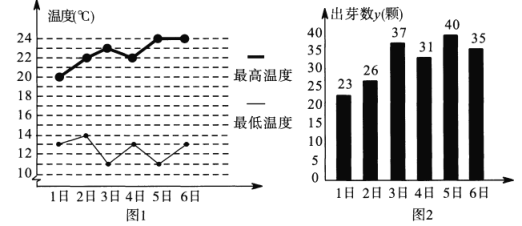
根据上述数据作出散点图,可知绿豆种子出芽数![]() (颗)和温差
(颗)和温差![]() (
(![]() )具有线性相关关系.
)具有线性相关关系.
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() (
(![]() )的回归方程
)的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为11![]() ,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
附: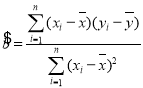
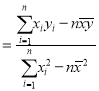 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
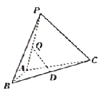
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕边AB翻转至
绕边AB翻转至![]() ,使面
,使面![]() 面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com