
(本题满分16分)设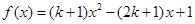 ,
, .
.
(1)若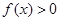 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,解不等式
时,解不等式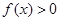 .
.
(1) ;
;
(2) .
.
(3)1)当 时,原不等式解为一切实数;
时,原不等式解为一切实数;
2)当 时,原不等式解为:
时,原不等式解为: .
.
3)当 时,原不等式的解为:
时,原不等式的解为: ;
;
4)当 时,原不等式的解为:
时,原不等式的解为: ;
;
5)当 时,
时,  。
。
解析试题分析:(1) 因为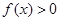 恒成立,所以k=-1时显然不成立;那么k应满足
恒成立,所以k=-1时显然不成立;那么k应满足 ,解之得即可求得k的取值范围.
,解之得即可求得k的取值范围.
(2)当 时,
时, 恒成立,设
恒成立,设 因为它在(1,2)上是增函数,故
因为它在(1,2)上是增函数,故 ,
,
从而当 时,
时, 恒成立,因而转化为常规的一元二次不等式
恒成立,因而转化为常规的一元二次不等式 对于
对于 恒成立来解决即可.
恒成立来解决即可.
(3) ,然后根据
,然后根据 和
和 和
和 再结合k<0分三种情况讨论解不等式即可.
再结合k<0分三种情况讨论解不等式即可.
(1)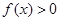 恒成立
恒成立 ……
……
 ,
, ……
……
(2)令 它在(1,2)上是增函数,故
它在(1,2)上是增函数,故 ,
,
从而当 时,
时, 恒成立 ……
恒成立 ……
即 对于
对于 恒成立,
恒成立, ;因为当
;因为当 时,
时, ,
,
所以 , ……
, ……
 ,
,
令 ,则
,则
 , ……
, ……
而 在
在 上是增函数,且
上是增函数,且 ,
, ,从而
,从而 . ……
. ……
(3) ,
,
1)当 时,
时, ,原不等式解为一切实数;
,原不等式解为一切实数;
2)当 时,
时, 原不等式解为:
原不等式解为: .
.
3)当 时,
时, ,
,
原不等式的解为: ;……
;……
4)当 时,原不等式的解为:
时,原不等式的解为: ;
;
5)当 时,
时,
原不等式的解为: ……
…… .
.
考点:一元二次不等式恒成立问题,换元法解不等式,分类讨论思想.
点评:(1)对于一元二次不等式f(x)>0恒成立问题,要满足开口向上,并且与x轴无交点,所以
二次项系数大于零,并且 .
.
(2)对于复杂类型的不等式问题可考虑采用换元法转化为常见不等式类型求解.
(3)对于含参的一元二次不等式要注意根据 的符号分类讨论求解.
的符号分类讨论求解.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
(14分)已知函数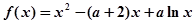 ,其中常数
,其中常数 。
。
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)当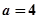 时,是否存在实数
时,是否存在实数 ,使得直线
,使得直线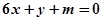 恰为曲线
恰为曲线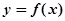 的切线?若存在,求出
的切线?若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)设定义在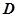 上的函数
上的函数 的图象在点
的图象在点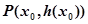 处的切线方程为
处的切线方程为 ,当
,当 时,若
时,若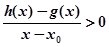 在
在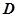 内恒成立,则称
内恒成立,则称 为函数
为函数 的“类对称点”。当
的“类对称点”。当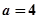 ,试问
,试问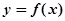 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知:函数y=f (x)的定义域为R,且对于任意的a,b∈R,都有f (a+b)=f (a)+f (b),且当x>0时,f (x)<0恒成立.
证明:(1)函数y=f (x)是R上的减函数.
(2)函数y=f (x)是奇函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com