Question

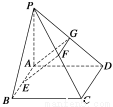
如图所示，在四棱锥P—ABCD中，底面ABCD是矩形，侧棱PA垂直于底面，E、F分别是AB、PC的中点，PA＝AD.

求证：(1)CD⊥PD；(2)EF⊥平面PCD.

 

Answer 1

见解析

【解析】

试题分析：1)证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高，中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等； (2)证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中的一条垂直于这个平面，则另一条也垂直于这个平面.解题时，注意线线、线面与面面关系的相互转化.

试题解析：(1)∵PA⊥底面ABCD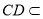，平面ABCD

∴CD⊥PA.

又矩形ABCD中，CD⊥AD，

∵ AD∩PA＝A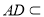，平面PAD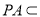，平面PAD

∴CD⊥平面PAD，

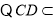平面PAD∴CD⊥PD.

(2)取PD的中点G，连结AG，FG.又∵G、F分别是PD、PC的中点，

∴

∴

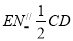
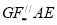
∴四边形AEFG是平行四边形，

∴AG∥EF.

∵PA＝AD，G是PD的中点，

∴AG⊥PD，∴EF⊥PD，

∵CD⊥平面PAD，AG?平面PAD.

∴CD⊥AG.∴EF⊥CD.

∵PD∩CD＝D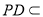， 平面PCD，CD平面PCD

∴EF⊥平面PCD.

考点：线线、线面与面面关系的相互转化、线面垂直