
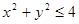 确定的平面区域为
确定的平面区域为 ,
,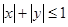 确定的平面区域为
确定的平面区域为
 内任取
内任取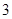 个整点,求这些整点中恰有
个整点,求这些整点中恰有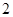 个整点在区域
个整点在区域 内的概率;
内的概率; 内任取
内任取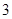 个点,记这
个点,记这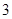 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望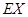 及方差
及方差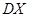 .
.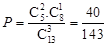 .(2)
.(2) 的分布列为:
的分布列为:   | 0 | 1 | 2 | 3 |
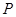 | 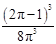 | 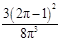 | 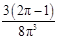 | 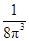 |
 的数学期望
的数学期望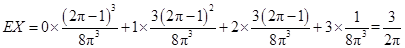 .
. ×2×2=2,在区域U内任取1个点,则该点在区域V内的概率为
×2×2=2,在区域U内任取1个点,则该点在区域V内的概率为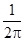
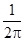 ) ,代入概率公式即可求得求X的分布列和数学期望和方差
) ,代入概率公式即可求得求X的分布列和数学期望和方差 的整点有
的整点有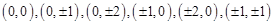 共有13个, ……2分
共有13个, ……2分 的整点为
的整点为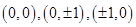 共有5个,∴
共有5个,∴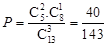 .……4分
.……4分 的面积为:
的面积为: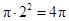 ,平面区域
,平面区域 的面积为:
的面积为: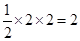 .
. 内任取1个点,则该点在区域
内任取1个点,则该点在区域 内的概率为
内的概率为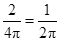 , ……1分
, ……1分 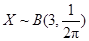 ,则
,则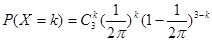 ,
,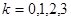 ……3分
……3分 的分布列为:
的分布列为:   | 0 | 1 | 2 | 3 |
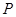 | 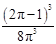 | 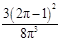 | 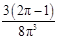 | 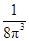 |
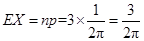 ,
,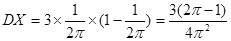 ……3分
……3分 的可能取值为
的可能取值为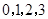 ,
, 
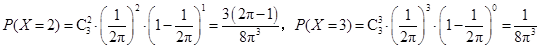 .
. 的分布列为:
的分布列为:   | 0 | 1 | 2 | 3 |
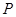 | 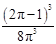 | 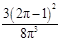 | 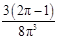 | 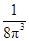 |
 的数学期望
的数学期望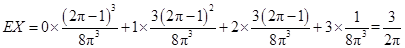


科目:高中数学 来源:不详 题型:单选题
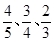 ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为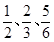 ,所有考试是否合格相互之间没有影响。
,所有考试是否合格相互之间没有影响。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
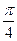 ;
;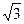 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
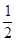 和
和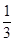 , 甲、乙两人各射击一次,有下列说法: ① 目标恰好被命中一次的概率为
, 甲、乙两人各射击一次,有下列说法: ① 目标恰好被命中一次的概率为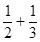 ;② 目标恰好被命中两次的概率为
;② 目标恰好被命中两次的概率为 ; ③ 目标被命中的概率为
; ③ 目标被命中的概率为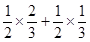 ; ④ 目标被命中的概率为
; ④ 目标被命中的概率为 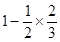 。以上说法正确的序号依次是
。以上说法正确的序号依次是 | A.②③ | B.①②③ | C.②④ | D.①③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,乙解出它的概率为
,乙解出它的概率为 ,丙解出它的概率为
,丙解出它的概率为 ,则
,则
|
 B.
B. C.
C.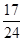 D.1
D.1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com