
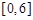 内任取两个数(可以相等),分别记为
内任取两个数(可以相等),分别记为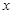 和
和 ,
,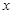 、
、 为正整数,求这两数中至少有一个偶数的概率;
为正整数,求这两数中至少有一个偶数的概率;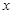 、
、
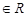 ,求
,求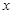 、
、 满足
满足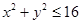 的概率.
的概率.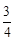 ;(2)
;(2) 
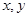 为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,“两个数
为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,“两个数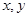 中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,利用概率公式解得
中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,利用概率公式解得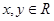 时,记事件总体为
时,记事件总体为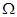 ,所求事件为B,则有
,所求事件为B,则有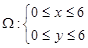 , B:
, B: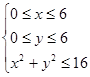 ,
,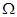 对应的区域为正方形,其面积为
对应的区域为正方形,其面积为 ,B对应的区域为四分之一圆,其面积为
,B对应的区域为四分之一圆,其面积为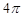 ,则由几何概型知道结论。
,则由几何概型知道结论。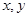 为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,如下:
为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,如下: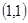 、
、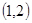 、
、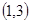 、
、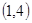 、
、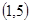 、
、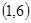 ;
;  、
、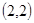 、
、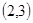 、
、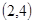 、
、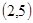 、
、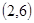 ;
;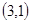 、
、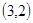 、
、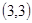 、
、 、
、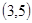 、
、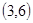 ;
; 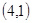 、
、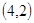 、
、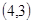 、
、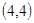 、
、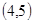 、
、 ;
; 、
、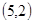 、
、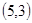 、
、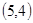 、
、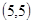 、
、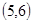 ;
; 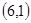 、
、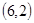 、
、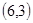 、
、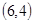 、
、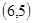 、
、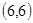 .
.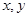 中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,由古典概型可知
中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,由古典概型可知 .
.  分
分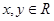 时,记事件总体为
时,记事件总体为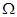 ,所求事件为B,则有
,所求事件为B,则有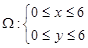 , B:
, B: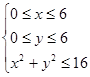 ,
,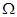 对应的区域为正方形,其面积为
对应的区域为正方形,其面积为 ,B对应的区域为四分之一圆,其面积为
,B对应的区域为四分之一圆,其面积为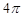 ,由几何概型可知
,由几何概型可知 .
. 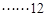 分
分

 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
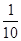 ,不堵车的概率为
,不堵车的概率为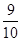 ;走公路Ⅱ堵车的概率为
;走公路Ⅱ堵车的概率为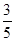 ,不堵车的概率为
,不堵车的概率为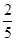 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
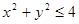 确定的平面区域为
确定的平面区域为 ,
,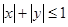 确定的平面区域为
确定的平面区域为
 内任取
内任取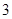 个整点,求这些整点中恰有
个整点,求这些整点中恰有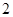 个整点在区域
个整点在区域 内的概率;
内的概率; 内任取
内任取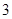 个点,记这
个点,记这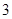 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望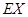 及方差
及方差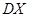 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
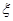 ,求
,求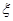 的数学期望
的数学期望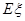 (即均值).
(即均值).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
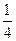 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。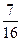 ,求走公路②堵的概率;
,求走公路②堵的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.622 | B.0.9 | C.0.0012 | D.0.0028 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com