
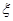 ,求
,求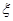 的数学期望
的数学期望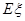 (即均值).
(即均值).科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
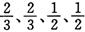 ,指标甲、乙、丙、丁被检测合格分别记4分、3分、2分、1分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
,指标甲、乙、丙、丁被检测合格分别记4分、3分、2分、1分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
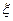 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.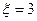 时的概率;
时的概率;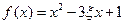 在区间
在区间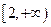 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com