
 =0.36.
=0.36.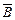 )=P(A)·P(
)=P(A)·P(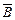 )
)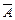 ·B)=P(
·B)=P(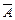 )P(B)=0.24,显然,“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生,即事件A·
)P(B)=0.24,显然,“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生,即事件A·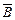 与
与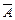 ·B互斥,所以恰有一人击中目标的概率是P(A·
·B互斥,所以恰有一人击中目标的概率是P(A·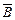 )+P(
)+P(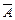 ·B)=0.24+0.24=0.48.
·B)=0.24+0.24=0.48.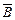 )+P(
)+P(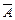 )·B]=0.
)·B]=0. 36+0.48=0.84
36+0.48=0.84

科目:高中数学 来源:不详 题型:解答题
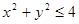 确定的平面区域为
确定的平面区域为 ,
,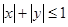 确定的平面区域为
确定的平面区域为
 内任取
内任取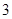 个整点,求这些整点中恰有
个整点,求这些整点中恰有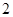 个整点在区域
个整点在区域 内的概率;
内的概率; 内任取
内任取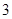 个点,记这
个点,记这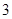 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望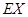 及方差
及方差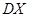 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
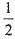 ,通晓中文和日语的概率为
,通晓中文和日语的概率为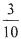 .若通晓中文和韩语的人数不超过3人.
.若通晓中文和韩语的人数不超过3人.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
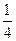 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。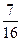 ,求走公路②堵的概率;
,求走公路②堵的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com