
已知函数f(x)=xe-x.
(1)求函数f(x)的单调区间和极值;
(2)当0<x<1时,f(x)>f ,求实数k的取值范围.
,求实数k的取值范围.
解:(1)由题知,f′(x)=(1-x)e-x(x∈R),当f′(x)>0时,x<1,当f′(x)<0时,x>1,
所以函数f(x)的单调递增区间为(-∞,1),单调递减区间为(1,+∞),
其极大值为f(1)=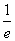 ,无极小值.
,无极小值.
(2)由题知,0<x<1,当k≤0时,
因为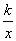 ≤0<x<1,由(1)知,函数f(x)在(-∞,1)上单调递增,
≤0<x<1,由(1)知,函数f(x)在(-∞,1)上单调递增,
所以f(x)>f ,符合题意;
,符合题意;
当0<k<1时,取x=k,可得f(k)>f(1),这与函数在(-∞,1)上单调递增不符;
当k≥1时,因为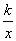 ≥
≥ >1,由(1)知,函数f(x)在(1,+∞)上单调递减,
>1,由(1)知,函数f(x)在(1,+∞)上单调递减,
所以f ≤f
≤f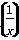 ,即只需证f(x)>f
,即只需证f(x)>f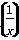 ,即证xe-x>
,即证xe-x> e-
e- ,
,
即ln x-x>-ln x- ,2ln x-x+
,2ln x-x+ >0,令h(x)=2ln x-x+
>0,令h(x)=2ln x-x+ (0<x<1),
(0<x<1),
则h′(x)=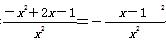 <0对0<x<1恒成立,所以h(x)为(0,1)上的减函数,所以h(x)>h(1)=0,
<0对0<x<1恒成立,所以h(x)为(0,1)上的减函数,所以h(x)>h(1)=0,
所以f(x)>f ,符合题意.
,符合题意.
综上知,实数k的取值范围是k∈(-∞,0]∪[1,+∞).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+1)=-f(x),且当x∈[0,1)时,f(x)=log2(x+1),给出下列命题:
①f(2 013)+f(-2 014)的值为0;
②函数f(x)在定义域上为周期是2的周期函数;
③直线y=x与函数f(x)的图象有1个交点;
④函数f(x)的值域为(-1,1).
其中正确命题的序号有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
一个射箭运动员在练习时只记射中9环和10环的成绩,未击中9环或10环就以0环记.该运动员在练习时击中10环的概率为a,击中9环的概率为b,既未击中9环也未击中10环的概率为c(a,b,c∈[0,1)),如果已知该运动员一次射箭击中环数的期望为9环,则当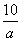 +
+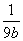 取最小值时,c的值为( )
取最小值时,c的值为( )
A.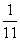 B.
B.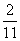 C.
C.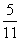 D.0
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)满足:对定义域内的任意x,都有kf(x+1)-f(x+k)>f(x),则称函数f(x)为“k度函数”,则下列函数中为“2度函数”的是( )
A.f(x)=2x+1 B.f(x)=ex
C.f(x)=ln x D.f(x)=xsin x
查看答案和解析>>
科目:高中数学 来源: 题型:
已知下列命题:
①设m为直线,α,β为平面,且m⊥β,则“m∥α”是“α⊥β”的充要条件;
②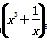 5的展开式中含x3的项的系数为60;
5的展开式中含x3的项的系数为60;
③设随机变量ξ~N(0,1),若P(ξ≥2)=p,则P(-2<ξ<0)= -p;
-p;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是(-∞,2).
其中真命题的序号是________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={x êx2+(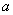 -1)x-
-1)x-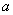 >0},B={x ê(x+
>0},B={x ê(x+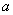 )(x+b)>0},其中
)(x+b)>0},其中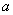 ≠b,M={x êx2-2x-3≤0},全集I=R.
≠b,M={x êx2-2x-3≤0},全集I=R.
(1)若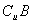 =M,求a、b的值;
=M,求a、b的值;
(2)若a>b>-1,求A∩B;
(3)若a2+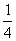 ∈
∈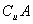 ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com