
分析 分析关于原点对称的两个点(x,y)点(-x,-y),是否都在曲线上,可判断①;分析关于直线y=x对称的两个点(x,y)点(y,x),是否都在曲线上,可判断②; 求出曲线C所围成的区域面积,可判断③.
解答 解:将方程中的x换成-x,y换成-y方程不变,所以曲线C关于原点对称,故①正确;
将方程中的x换成y,y换成x,方程变为y4+x2=1与原方程不同,故②错误;
在曲线C上任取一点M(x0,y0),x04+y02=1,
∵|x0|≤1,
∴x04≤x02,
∴x02+y02≥x04+y02=1,即点M在圆x2+y2=1外,
故③正确;
故正确的结论的序号是:①③,
故答案为:①③
点评 本题考查的知识点是曲线Cx4+y2=1的图象和性质,对称性的判断,面积的求解,难度中档.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
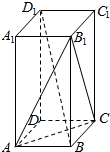
| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 0 | D. | ±$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com