
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
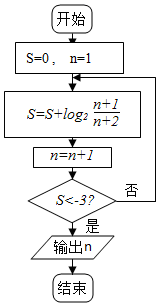
分析 通过分析循环,推出循环规律,利用循环的次数,求出输出结果.
解答 解:模拟程序的运行,可得
S=0,n=1
第1次执行循环,S=log2$\frac{2}{3}$,n=2
不满足条件S<-3,第2次执行循环,S=log2$\frac{2}{3}$+log2$\frac{3}{4}$,n=3
不满足条件S<-3,第3次执行循环,S=log2$\frac{2}{3}$+log2$\frac{3}{4}$+log2$\frac{4}{5}$,n=4
…
不满足条件S<-3,第n次循环:S=log2$\frac{2}{3}$+log2$\frac{3}{4}$+log2$\frac{4}{5}$+…+log2$\frac{n}{n+1}$=log2$\frac{2}{n+1}$,n=n+1;
令log2$\frac{2}{n+1}$<-3,解得n>15.
∴输出的结果是n+1=16.
故选:B.
点评 本题考查程序框图的应用,数列的应用,考查分析问题解决问题的能力,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
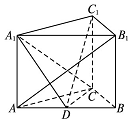 如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3D为AB的中点,AB1⊥A1C
如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3D为AB的中点,AB1⊥A1C查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2人 | B. | 3人 | C. | 2人或3人 | D. | 4人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
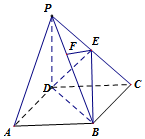 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
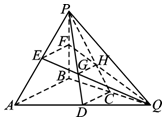 已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com