
【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: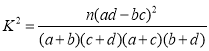 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
科目:高中数学 来源: 题型:
【题目】中国男子篮球甲级联赛的规则规定:每场比赛胜者得2 分, 负者得1 分(每场比赛, 即使通过加时赛也必须分出胜负).某男篮甲级队实力强劲, 每场比赛获胜的概率为![]() 、失利的概率为
、失利的概率为![]() .求该队在赛程中间通过若干场比赛获得n 分的概率(设该队这一赛季的全部比赛场次数为S,这里0<n ≤S).
.求该队在赛程中间通过若干场比赛获得n 分的概率(设该队这一赛季的全部比赛场次数为S,这里0<n ≤S).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 且x,
且x,![]() .
.
(1)判断![]() 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;
(2)若不等式![]() 在
在![]() 上恒成立,试求实数a的取值范围;
上恒成立,试求实数a的取值范围;
(3)![]() 的值域为
的值域为![]() 函数
函数![]() 在
在![]() 上的最大值为M,最小值为m,若
上的最大值为M,最小值为m,若![]() 成立,求正数a的取值范围.
成立,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体 ABCD-A1B1C1D1 的棱长为 1 , E 、F 分别是棱 AB 、BC上的动点 ,且AE = BF .求直线 A1E 与C1F 所成角的最小值(用反三角函数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com