
【题目】已知椭圆![]() 的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,
的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,![]() 最大值为1.
最大值为1.
(1)求椭圆C的方程;
(2)不过点F2的直线l:y=kx+m(m≠0)交椭圆C于A,B两点.
①若![]() ,且
,且![]() ,求m的值.
,求m的值.
②若x轴上任意一点到直线AF2与BF2距离相等,求证:直线l过定点,并求出该定点的坐标.
【答案】(1)![]() .(2)①
.(2)①![]() ,②
,②![]() .
.
【解析】
(1)根据题意,可求得c=1,b=1,进而求得a,由此得到椭圆方程;
(2)①联立方程,得到k与m的不等关系,及两根的关系,表示出弦长AB及点O到直线AB的距离,由此建立等式解出即可;②依题意,k1+k2=0,由此可得到k与m的等量关系,进而求得定点.
解:(1)由抛物线的方程y2=4x得其焦点为(1,0),则c=1,
当点M为椭圆的短轴端点时,△MF1F2面积最大,此时![]() ,则b=1,
,则b=1,
∴![]() ,故椭圆的方程为
,故椭圆的方程为![]() ;
;
(2)联立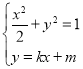 得,(1+2k2)x2+4kmx+2m2﹣2=0,
得,(1+2k2)x2+4kmx+2m2﹣2=0,
△=16k2m2﹣4(2k2+1)(2m2﹣2)=8(2k2﹣m2+1)>0,得1+2k2>m2(*),
设A(x1,y1),B(x2,y2),则![]() ,
,
①∵m≠0且![]() ,代入(*)得,0<m2<2,
,代入(*)得,0<m2<2,
![]() ,
,
设点O到直线AB的距离为d,则![]() ,
,
∴![]() ,
,
∴m2=1∈(0,2),则m=±1;
②![]() ,
,
由题意,k1+k2=0,
∴![]() ,即2kx1x2+(m﹣k)(x1+x2)﹣2m=0,
,即2kx1x2+(m﹣k)(x1+x2)﹣2m=0,
∴![]() ,
,
解得m=﹣2k,
∴直线l的方程为y=k(x﹣2),故直线l恒过定点,该定点坐标为(2,0).


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】设递增等比数列{an}的前n项和为Sn,且a2=3,S3=13,数列{bn}满足b1=a1,点P(bn,bn+1)在直线x﹣y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生自主创业,经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润800元,未售出的产品,每
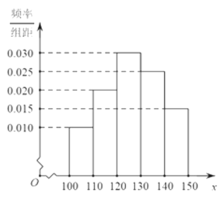
该产品获利润800元,未售出的产品,每![]() 亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了
亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (单位:
(单位:![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于94000元的概率;
不少于94000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的均值.
的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了200位高三学生的成绩进行统计分析得到如图所示频率分布直方图:
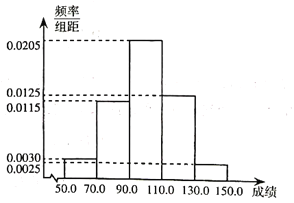
(1)计算这些学生成绩的平均值![]() 及样本方差
及样本方差![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)由频率分布直方图认为,这次成绩X近似服从正态分布![]() ,其中μ近似为样本平均数
,其中μ近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)求![]() ;
;
(ii)从高三学生中抽取10位学生进行面批,记![]() 表示这10位学生成绩在
表示这10位学生成绩在![]() 的人数,利用(i)的结果,求数学期望
的人数,利用(i)的结果,求数学期望![]() .
.
附:![]() ;
;
若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象为C,下面结论正确的是( )
的图象为C,下面结论正确的是( )
A.函数f(x)的最小正周期是2π.
B.函数f(x)在区间![]() 上是递增的
上是递增的
C.图象C关于点![]() 对称
对称
D.图象C由函数g(x)=sin2x的图象向左平移![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线C:y2=8x上一点A到焦点F的距离为6,若点P为抛物线C准线上的动点,则|OP|+|AP|的最小值为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com