
【题目】某大学生自主创业,经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润800元,未售出的产品,每
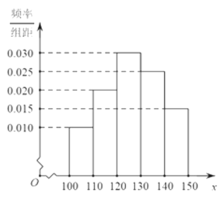
该产品获利润800元,未售出的产品,每![]() 亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了
亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (单位:
(单位:![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于94000元的概率;
不少于94000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的均值.
的均值.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 在以
在以![]() 为圆心,1为半径的圆
为圆心,1为半径的圆![]() 上,且
上,且![]() .
.
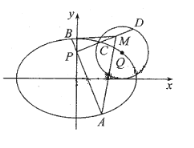
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为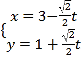 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为(3,1),求
的坐标为(3,1),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,
的一个焦点与抛物线y2=4x的焦点相同,F1,F2为C的左右焦点,M为C上任意一点,![]() 最大值为1.
最大值为1.
(1)求椭圆C的方程;
(2)不过点F2的直线l:y=kx+m(m≠0)交椭圆C于A,B两点.
①若![]() ,且
,且![]() ,求m的值.
,求m的值.
②若x轴上任意一点到直线AF2与BF2距离相等,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
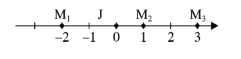
【题目】本学期开学前后,国务院下发了《新一代人工智能发展规划》,要求从小学教育,中学教育,到大学院校,逐步新增人工智能课程,建设全国人才梯队,凸显了我国抢占人工智能新高地的决心和信心.如图,三台机器人![]() 、
、![]() 、
、![]() 和检测台
和检测台![]() (位置待定)(
(位置待定)(![]() 与
与![]() 、
、![]() 、
、![]() 共线但互不重合),三台机器人需把各自生产的零件送交
共线但互不重合),三台机器人需把各自生产的零件送交![]() 处进行检测,送检程序如下:当
处进行检测,送检程序如下:当![]() 把零件送达
把零件送达![]() 处时,
处时,![]() 即刻自动出发送检;当
即刻自动出发送检;当![]() 把零件送达
把零件送达![]() 处时,
处时,![]() 即刻自动出发送检.设
即刻自动出发送检.设![]() 、
、![]() 的送检速度的大小为2,
的送检速度的大小为2,![]() 的送检速度大小为1.则三台机器人
的送检速度大小为1.则三台机器人![]() 、
、![]() 、
、![]() 送检时间之和的最小值为( ).
送检时间之和的最小值为( ).
A.8B.6C.5D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com