
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)证明:(i)![]() ;
;
(ii)对任意![]() ,
,![]() 对
对![]() 恒成立.
恒成立.
【答案】(1)![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,
,![]() 的单调递减区间为
的单调递减区间为![]() . (2)(i)证明见解析(ii)证明见解析
. (2)(i)证明见解析(ii)证明见解析
【解析】
(1)将![]() 代入函数解析式,并求得导函数,由导函数的符号即可判断
代入函数解析式,并求得导函数,由导函数的符号即可判断![]() 的单调区间;
的单调区间;
(2)(i)构造函数![]() 并求得
并求得![]() ,利用
,利用![]() 的单调性求得最大值,即可证明不等式成立.;(ii)由(i)可知将不等式变形可得
的单调性求得最大值,即可证明不等式成立.;(ii)由(i)可知将不等式变形可得![]() 成立,构造函数
成立,构造函数![]() ,因式分解后解一元二次不等式即可证明
,因式分解后解一元二次不等式即可证明![]() 对
对![]() 恒成立.
恒成立.
(1)若![]() ,
,![]() (
(![]() ),
),
令![]() ,得
,得![]() 或
或![]() , 则
, 则![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
令![]() ,得
,得![]() ,则
,则![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)证明:(i)设![]() ,
,
则![]() (
(![]() ),
),
令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() .
.
故![]() ,
,
从而![]() ,即
,即![]() .
.
(ii)函数![]()
由(i)可知![]()
即![]() ,所以
,所以![]() ,当
,当![]() 时取等号;
时取等号;
所以当![]() 时,则
时,则![]()
若![]() ,令
,令![]()
则![]() ,
,
当![]() 时,
时,![]() .
.
则当![]() 时,
时,![]() ,
,
故对任意![]() ,
,![]() 对
对![]() 恒成立.
恒成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程.
的轨迹方程.
(2)设点![]() ,
,![]() 是
是![]() 的轨迹上异于顶点的任意两点,以
的轨迹上异于顶点的任意两点,以![]() 为直径的圆过点
为直径的圆过点![]() .求证直线
.求证直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 为抛物线
为抛物线![]() 过焦点
过焦点![]() 的弦,已知以
的弦,已知以![]() 为直径的圆与
为直径的圆与![]() 相切于点
相切于点![]() .
.
(1)求![]() 的值及圆的方程;
的值及圆的方程;
(2)设![]() 为
为![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,右表是对 100 辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
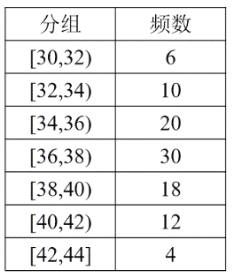
(Ⅰ)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(Ⅱ)用分层抽样的方法从行车里程在区间[38,40)与[40,42)的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在[40,42)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() 时,
时,![]() 在
在![]() 上是单调递增函数,求
上是单调递增函数,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调区间;
的单调区间;
(3)对于任意给定的正实数![]() ,证明:存在实数
,证明:存在实数![]() ,使得
,使得![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com