
【题目】已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 在以
在以![]() 为圆心,1为半径的圆
为圆心,1为半径的圆![]() 上,且
上,且![]() .
.
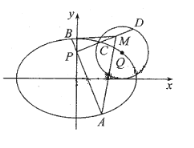
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(1) ![]() ;(2)
;(2) 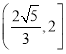 .
.
【解析】
(1) 由![]() 在以
在以![]() 为圆心,1为半径的圆
为圆心,1为半径的圆![]() 上,可知圆
上,可知圆![]() 的方程为
的方程为![]() ,由此圆与
,由此圆与![]() 轴相切,可得切点坐标为
轴相切,可得切点坐标为![]() ,则可得出
,则可得出![]() ,由
,由![]() 由两点间距离公式可求得
由两点间距离公式可求得![]() 即求出
即求出![]() 的值,进而求得
的值,进而求得![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程.
的方程.
(2)因为![]() 设
设![]() ,则
,则![]() ,
,![]() 与椭圆联立,得
与椭圆联立,得![]() ,由此利用弦长公式可求得
,由此利用弦长公式可求得![]() 、又
、又![]() .可知
.可知![]() ,
,![]() 到
到![]() 的距离即
的距离即![]() 到
到![]() 的距离,利用点到直线距离公式即可求得距离,通过面积公式可得
的距离,利用点到直线距离公式即可求得距离,通过面积公式可得![]() ,令
,令![]() ,构造函数
,构造函数![]() 化简、借助单调性即可求出
化简、借助单调性即可求出![]() 面积的取值范围.
面积的取值范围.
(1) 圆![]() 的方程为
的方程为![]() ,此圆与
,此圆与![]() 轴相切,则切点为
轴相切,则切点为![]() 即
即![]() ,
,
所以![]() ,又
,又![]()
所以![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2) 当![]() 平行
平行![]() 轴的时候,
轴的时候,![]() 与圆
与圆![]() 无公共点,从而
无公共点,从而![]() 不存在;设
不存在;设![]() ,则
,则![]() .
.
由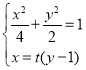 ,消去
,消去![]() 得
得![]()
则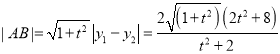 又圆心
又圆心![]() 到
到![]() 的距离
的距离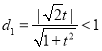 得
得![]() .又
.又![]() .
.![]() 到
到![]() 的距离即
的距离即![]() 到
到![]() 的距离,设为
的距离,设为![]() ,即
,即 .
.
![]() 面积
面积![]() 令
令![]()
则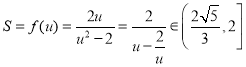
![]() 面积的取值范围为
面积的取值范围为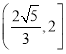 .
.


科目:高中数学 来源: 题型:
【题目】某控制器中有一个易损部件,该部件由两个电子元件按图1方式连接而成.已知这两个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常工作相互独立.(一个月按30天算)
,且各个元件能否正常工作相互独立.(一个月按30天算)
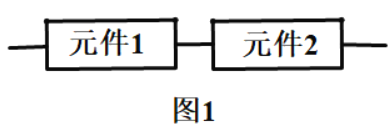
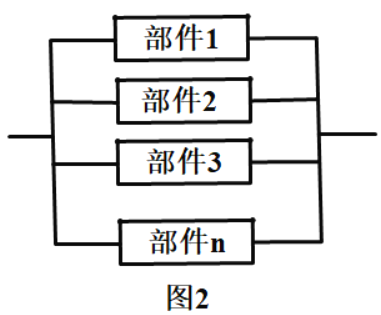
(1)求该部件的使用寿命达到一个月及以上的概率;
(2)为了保证该控制器能稳定工作,将若干个同样的部件按图2连接在一起组成集成块.每一个部件是否能正常工作相互独立.某开发商准备大批量生产该集成块,在投入生产前,进行了市场调查,结果如下表:
集成块类型 |
| 成本 | 销售金额 |
Ⅰ |
|
|
|
Ⅱ |
|
|
|
Ⅲ |
|
|
|
其中![]() 是集成块使用寿命达到一个月及以上的概率,
是集成块使用寿命达到一个月及以上的概率,![]() 为集成块使用的部件个数.报据市场调查,试分析集成块使用的部件个数为多少时,开发商所得利润最大?并说明理由.
为集成块使用的部件个数.报据市场调查,试分析集成块使用的部件个数为多少时,开发商所得利润最大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列命题:
,下列命题:
①![]() 的定义域为
的定义域为![]() ;
;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上单调递增;
上单调递增;
④若实数![]() 满足
满足![]() ,则
,则![]() ;
;
⑤设函数![]() 在上的最大值为
在上的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() .
.
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设递增等比数列{an}的前n项和为Sn,且a2=3,S3=13,数列{bn}满足b1=a1,点P(bn,bn+1)在直线x﹣y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为
的半径为![]() ,点
,点![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新政策的实施,海淘免税时代于2016年4月8日正式结束,新政策实施后,海外购物的费用可能会增加.为了解新制度对海淘的影响,某网站调查了喜欢海淘的1000名网友,其态度共有两类:第一类是会降低海淘数量,共有400人,第二类是不会降低海淘数量,共有600人,若从这1000人中按照分层抽样的方法抽取10人后进行打分,其打分的茎叶图如下图所示,图中有数据缺失,但已知“第一类”和“第二类”网民打分的均值相等,则“第一类”网民打分的方差为( )
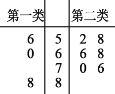
A.159B.179C.189D.209
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生自主创业,经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润800元,未售出的产品,每
该产品获利润800元,未售出的产品,每![]() 亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了
亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (单位:
(单位:![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
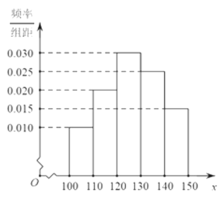
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于94000元的概率;
不少于94000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的均值.
的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com