
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
分析 由已知结合bn=$\frac{{a}_{n+1}}{{a}_{n}}$,得到a21=b1b2…b20,结合b10b11=2015${\;}^{\frac{1}{10}}$,以及等比数列的性质求得答案.
解答 解:由bn=$\frac{{a}_{n+1}}{{a}_{n}}$,且a1=1,得b1=$\frac{{a}_{2}}{{a}_{1}}={a}_{2}$,
b2=$\frac{{a}_{3}}{{a}_{2}}$,∴a3=a2b2=b1b2,
b3=$\frac{{a}_{4}}{{a}_{3}}$,∴a4=a3b3=b1b2b3,
…
an=b1b2…bn-1.
∴a21=b1b2…b20.
∵数列{bn}为等比数列,
∴a21=(b1b20)(b2b19)…(b10b11)=$(201{5}^{\frac{1}{10}})^{10}=2015$.
故选:B.
点评 本题考查了数列递推式,考查了等比数列的性质,是中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-1,7) | C. | (-1,10) | D. | (-10,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
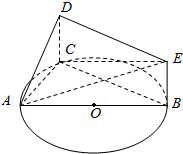 如图,AB是圆O的直径,C是圆O上异于A、B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A、B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{13}}}{13}$ | B. | $\frac{{\sqrt{13}}}{13}$ | C. | $\frac{1}{13}$ | D. | $\frac{2}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com