
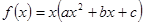 (
(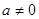 )在
)在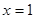 和
和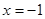 处均有极值,则下列点中一定在
处均有极值,则下列点中一定在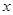 轴上的是( )
轴上的是( )A.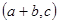 | B.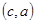 | C.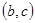 | D.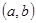 |
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:不详 题型:解答题
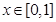 ,总有
,总有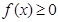 ;②
;②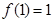 ;③若
;③若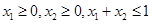 ,则有
,则有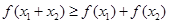 成立.
成立. 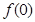 的值;(2) 函数
的值;(2) 函数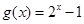 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明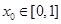 ,使得
,使得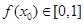 ,且
,且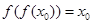 ,求证:
,求证:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |

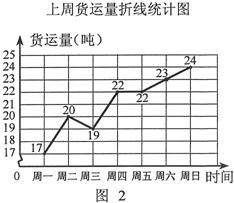
 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与  的函数关系式(不必写出
的函数关系式(不必写出 的取值范围),及
的取值范围),及 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com