Question

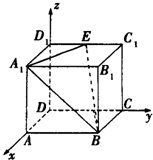
3．如图，在空间直角坐标系D-xyz中，四棱柱ABCD-A₁B₁C₁D₁为长方体，AA₁=AB=2AD，点E为C₁D₁的中点，则二面角B₁-A₁B-E的余弦值为（　　）

• A． $-\frac{{\sqrt{3}}}{3}$
• B． $-\frac{{\sqrt{3}}}{2}$
• C． $\frac{{\sqrt{3}}}{3}$
• D． $\frac{{\sqrt{3}}}{2}$

Answer 1

分析 分别求出两个平面的法向量，再求出其夹角即可得出结论．

解答 解：设A₁（1，0，2），B₁（1，2，2），C₁（0，2，2），D₁（0，0，2），B（1，2，0），
∵E，F分别为C₁D₁、A₁B的中点，∴E（0，1，2），
∴$\overrightarrow{{A}_{1}E}$=（-1，1，0），$\overrightarrow{{A}_{1}B}$=（0，2，-2），
设$\overrightarrow{m}$=（x，y，z）是平面A₁BE的一个法向量，
∴$\left\{\begin{array}{l}{-x+y=0}\\{2y-2z=0}\end{array}\right.$，
取x=1，得平面A₁BE的一个法向量为$\overrightarrow{m}$=（1，1，1），
又DA⊥平面A₁B₁B，
∴$\overrightarrow{DA}$=（1，0，0）是平面A₁B₁B的一个法向量，且二面角B₁-A₁B-E为锐二面角，
∴二面角B₁-A₁B-E的余弦值为$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$．
故选C．

点评 熟练掌握通过建立空间直角坐标系，利用两个平面的法向量的夹角得出二面角的大小的方法是解题的关键．