练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某年级先后举办了数学、音乐讲座，其中听数学讲座43人，听音乐讲座34人，还有15人同时听了数学和音乐，则听讲座的人数为62人．

    分析 根据题意，设听数学的学生为集合A，听音乐的学生为集合B，由题意可得card（A）=43，card（B）=34，且card（A∩B）=15；由集合的交、并集的元素数目关系可得card（A∪B）=card（A）+card（B）-card（A∩B），计算可得答案．

    解答 解：根据题意，设听数学的学生为集合A，听音乐的学生为集合B，
    则card（A）=43，card（B）=34，且card（A∩B）=15；
    则card（A∪B）=card（A）+card（B）-card（A∩B）=43+34-15=62；
    即听讲座的人数为62；
    故答案为：62．

    点评 本题考查集合的交集运算，关键是转化思路，把原问题转化为集合的交集、并集问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．在平面直角坐标系中，直线$\sqrt{2}x-y+m=0$不过原点，且与椭圆$\frac{y^2}{4}+\frac{x^2}{2}=1$有两个不同的公共点A，B．
    （Ⅰ）求实数m取值所组成的集合M；
    （Ⅱ）是否存在定点P使得任意的m∈M，都有直线PA，PB的倾斜角互补．若存在，求出所有定点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

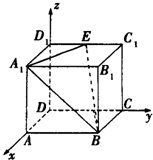    3．如图，在空间直角坐标系D-xyz中，四棱柱ABCD-A1B1C1D1为长方体，AA1=AB=2AD，点E为C1D1的中点，则二面角B1-A1B-E的余弦值为（　　）
    A．$-\frac{{\sqrt{3}}}{3}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{{\sqrt{3}}}{3}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知y=lnx+x，x∈[1，e]，则y的最大值为（　　）
    A．1B．e-1C．e+1D．e

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．要得到函数$y=\frac{{\sqrt{2}}}{2}sinx+\frac{{\sqrt{2}}}{2}cosx+1$的图象，需要把函数y=sinx的图象（　　）
    A．向右平移$\frac{π}{4}$个单位，再向上平移1个单位
    B．向左平移$\frac{π}{4}$个单位，再向上平移1个单位
    C．向左平移$\frac{π}{4}$个单位，再向下平移1个单位
    D．向右平移$\frac{π}{4}$个单位，再向下平移1个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知定义在区间[0，2]上的两个函数f（x）和g（x），其中f（x）=x2-2ax+4（a≥1），g（x）=ln（x+1）-ln3+$\frac{4}{3}$．
    （1）求函数y=f（x）的最小值m（a）；
    （2）若对任意x1、x2∈[0，2]，f（x2）＞g（x1）恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知sinα+cosα=-$\frac{1}{5}$，α∈（0，π），则tanα的值为（　　）
    A．-$\frac{4}{3}$或-$\frac{3}{4}$B．-$\frac{4}{3}$C．-$\frac{3}{4}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若点A（ab，a+b）在第一象限内，则直线bx+ay-ab=0不经过第三象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知y=f（x）为二次函数，且f（0）=-5，f（-1）=-4，f（2）=-5，求此二次函数的解析式．

    查看答案和解析>>

    同步练习册答案