
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
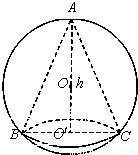
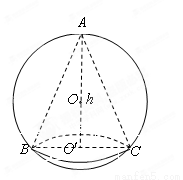
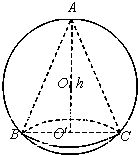
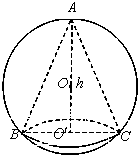 如图,已知球的半径为定值R,球内接圆锥的高为h(h>R),体积为V,
如图,已知球的半径为定值R,球内接圆锥的高为h(h>R),体积为V,查看答案和解析>>
科目:高中数学 来源:高三数学教学与测试 题型:044
已知球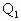 的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠
的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠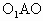 =θ.
=θ.
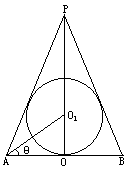
(1)试用R,θ表示圆锥底面半径r,母线l和全面积S;
(2)当θ为何值时,圆锥全面积取最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源:2013届四川成都七中高二下学期期中考试文科数学试卷(解析版) 题型:解答题
如图,已知球的半径为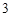 ,球内接圆锥的高为
,球内接圆锥的高为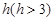 ,体积为
,体积为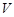 ,
,
(1)写出以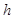 表示
表示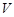 的函数关系式
的函数关系式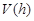 ;
;
(2)当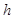 为何值时,
为何值时,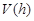 有最大值,并求出该最大值.
有最大值,并求出该最大值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com