【选修4-4：坐标系与参数方程】
在平面直角坐标系
中，曲线
的参数方程为
（
为参数）以原点
为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
.若直线
与曲线
交于
，求线段
的长.
名校课堂系列答案科目：高中数学 来源：2016届河南省洛阳市高三下学期第二次模拟理科数学试卷（解析版） 题型：解答题
4月23日是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”
（1）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
（2）将频率视为概率，现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书谜”的人数为
，若每次抽取的结果是相互独立的，求的分布列，期望
和方差
.
附：
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源：2016届江苏南通市高三下学期第三次调研考试数学试卷（解析版） 题型：解答题
某宾馆在装修时，为了美观，欲将客房的窗户设计成半径为
的圆形，并用四根木条将圆分成如图所示的9个区域，其中四边形
为中心在圆心的矩形，现计划将矩形
区域设计为可推拉的窗口.
（1）若窗口为正方形，且面积大于
（木条宽度忽略不计），求四根木条总长的取值范围；
（2）若四根木条总长为
，求窗口面积的最大值.
查看答案和解析>>
科目：高中数学 来源：2016届江苏省苏北三市高三最后一次模拟考试数学试卷（解析版） 题型：解答题
在数列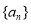
中，已知
，
.
（1）求数列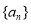的通项公式；
（2）求满足
的正整数
的值；
（3）设数列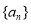的前
项和为
，问是否存在正整数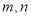
，使得
？若存在，求出所有的正整数对
；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源：2015-2016学年天津市等六校高二上学期期末理科数学卷（解析版） 题型：解答题
如图，在四棱锥
中，底面
为菱形，
，
为
的中点.
(Ⅰ)若
，求证：平面
平面
；
(Ⅱ)点
在线段
上，
，若平面
平面
，且
，求二面角
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.
的值；
时，试猜想所有
的最大公约数，并证明.
是定义在
上的偶函数，则
.
满足
（
为虚数单位），则
.
满足
，则
的值为 .