正方体ABCD-A/B/C/D/的棱长为8cm,M,N,P分别是AB,A/D/,BB/棱的中点.
(1)画出过M,N,P三点的平面与平面A/B/C/D/及平面BB/C/C的交线,并说明画法的依据;
(2)设过M,N,P三点的平面与B/C/交于点Q,求PQ的长.
分析:(1)利用直线上的两个点在平面内,则直线在平面内;若一条直线在一个平面内又在另一个平面内,则直线是交线
(2)利用相似三角形的对应边成比例,求出B′Q;据直角三角形的勾股定理求出PQ长.
解答: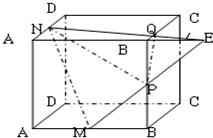
(本小题满分10分)
解:(1)如图,延长MP、A
/B
/相交于点E,连接NE,交B
/C
/于Q,
连接QP,则NE为平面MNP与平面A
/B
/C
/D
/的交线,PQ为平面MNP
与平面BB
/C
/C的交线;
理由:∵E∈直线MP,且E∈平面MNP,且E∈平面A′B′C′D′,
同理,N∈平面MNP,且N∈平面A′B′C′D′,所以,NE为平面MNP与平面A
/B
/C
/D
/的交线,
显然,PQ为平面MNP与平面BB
/C
/C的交线;(5分)
(2)由已知和(1)得MB=B
/E=4,又△EB′Q∽△EA′N,所以,B′Q=
,又B′P=4,
所以,PQ=
(5分)
点评:本题考查直线与平面的关系:直线上的两个点在平面内,直线在平面内;
相似三角形的对应边成比例、直角三角形的勾股定理.

 (本小题满分10分)
(本小题满分10分)

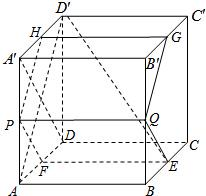 如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.
如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′. (2011•蓝山县模拟)如图,在正方体ABCD-A′B′C′D′中,异面直线BD与B′C所成角为
(2011•蓝山县模拟)如图,在正方体ABCD-A′B′C′D′中,异面直线BD与B′C所成角为