
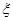 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求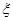 的分布列和数学期望
的分布列和数学期望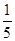 ;(2)
;(2)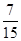 ;(3)分布列(略),
;(3)分布列(略),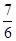 .
.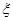 可能取值为0,1,2,3,注意分别对应概率的计算.
可能取值为0,1,2,3,注意分别对应概率的计算.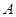 ,
,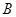 .
.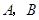 相互独立,且
相互独立,且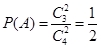 ,
,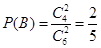 . 2分
. 2分 . 4分
. 4分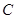 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件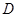 .则
.则 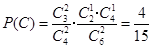 ,
,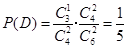 . 6分
. 6分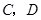 互斥,故取出的4个球中恰有1个红球的概率为
互斥,故取出的4个球中恰有1个红球的概率为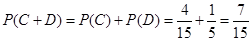 . 8分
. 8分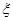 可能的取值为
可能的取值为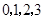 .
.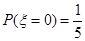 ,
,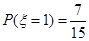 ,
, 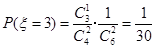 .
.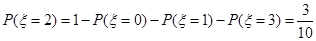 .
.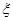 的分布列为
的分布列为 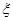 | 0 | 1 | 2 | 3 |
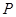 | 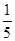 | 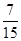 | 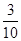 | 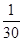 |
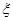 的数学期望
的数学期望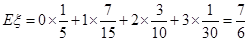 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
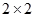 列联表:
列联表: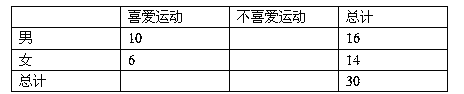
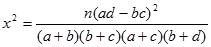 (其中
(其中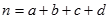 )
)| | 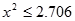 | 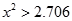 | 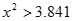 | 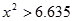 |
| 是否有关联 | 没有关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
| 届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 主办国家 | 联邦德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大利亚 | 希腊 | 中国 |
| 上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
| 当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
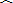 |
| y |
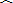 |
| b |
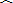 |
| a |
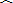 |
| b |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 主食蔬菜 | 主食肉类 | 合计 | |
| 50岁以下 | |||
| 50岁以上 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0] | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
| 38 |
| 9 |
| n(ad-bc)2 |
| (a+b)(b+c)(a+c)(b+d) |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com