
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
| 38 |
| 9 |
| n(ad-bc)2 |
| (a+b)(b+c)(a+c)(b+d) |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
科目:高中数学 来源:不详 题型:解答题
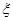 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求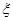 的分布列和数学期望
的分布列和数学期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
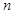 及天数如下表:
及天数如下表:售出个数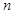 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.y=0.8x+3 | B.y=-1.2x+7.5 |
| C.y=1.6x+0.5 | D.y=1.3x+1.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
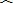 |
| y |
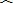 |
| b |
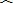 |
| a |
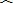 |
| a |
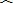 |
| b |
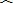 |
| b |
| |||||
|
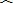 |
| a |
| . |
| y |
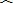 |
| b |
| . |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 患心脏病 | 患其它病 | 合计 | |
| 高血压 | 20 | 10 | 30 |
| 不高血压 | 30 | 50 | 80 |
| 合计 | 50 | 60 | 110 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 k2=
k2=| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| ^y=3+2x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 一次 购物量 | 1至 4件 | 5至 8件 | 9至 12件 | 13至 16件 | 17件及 以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间 (分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com