
【题目】设A,B为函数![]() 图象上相异两点,且A,B的横坐标之积为常数
图象上相异两点,且A,B的横坐标之积为常数![]() ,若
,若![]() 在A,B两点处的切线存在交点,则称这个交点为函数
在A,B两点处的切线存在交点,则称这个交点为函数![]() 的“
的“![]() 点”。
点”。
(1)求函数![]() 的“
的“![]() 点”的纵坐标的取值范围;
点”的纵坐标的取值范围;
(2)判断函数![]() 的
的![]() 点”在哪个象限,并说明理由.
点”在哪个象限,并说明理由.
科目:高中数学 来源: 题型:
【题目】驾驶员“科目一”考试,又称科目一理论考试、驾驶员理论考试,是机动车驾驶证考核的一部分.根据《机动车驾驶证申领和使用规定》,考试内容包括驾车理论基础、道路安全法律法规、地方性法规等相关知识.考试形式为上机考试100道题,90分及以上过关.考试规则是:若上午第一次考试未通过,当场可以立刻补考一次;如果补考还没过,那么出了考场缴费后,下午可以再考,若还未通过可再补考一次.已知小王每一次通过考试的概率均为0.5,且每一场考试与补考是否通过相互独立,则当天小王通过“科目一”考试的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高。2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化。下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
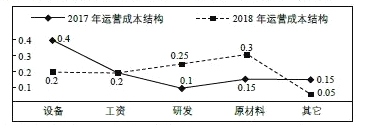
A.该企业2018年设备支出金额是2017年设备支出金额的一半
B.该企业2018年支付工资金额与2017年支付工资金额相当
C.该企业2018年用于研发的费用是2017年用于研发的费用的五倍
D.该企业2018年原材料的费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)现给出三个条件:①![]() ; ②
; ②![]() ;③
;③![]() .
.
试从中选出两个可以确定![]() 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求![]() 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,方程![]() 的图形为如图所示的“幸运四叶草”,又称为玫瑰线.
的图形为如图所示的“幸运四叶草”,又称为玫瑰线.

(1)当玫瑰线的![]() 时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
(2)求曲线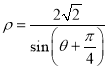 上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分而不必要条件
”的充分而不必要条件
C.若![]() 且
且![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() “存在
“存在![]() ,使得
,使得![]() ”,则非
”,则非![]() “任意
“任意![]() ,均有
,均有![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知二次函数![]() (
(![]() 、
、![]() 、
、![]() 均为实常数,
均为实常数,![]() )的最小值是0,函数
)的最小值是0,函数![]() 的零点是
的零点是![]() 和
和![]() ,函数
,函数![]() 满足
满足![]() ,其中
,其中![]() ,为常数.
,为常数.
(1)已知实数![]() 、
、![]() 满足、
满足、![]() ,且
,且![]() ,试比较
,试比较![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com