
【题目】在![]() 中,若
中,若![]() ,则
,则![]() 的形状是( )
的形状是( )
A.等腰三角形B.直角三角形
C.等腰三角形或直角三角形D.等腰直角三角形
【答案】B
【解析】
由sinC(cosA+cosB)=sinA+sinB,利用三角形内角和定理及其诱导公式可得:sinCcosA+sinCcosB=sin(B+C)+sin(A+C)展开化为sinBcosC+sinAcosC=0,可得cosC=0,C∈(0,π).即可得出.
在△ABC中,∵sinC(cosA+cosB)=sinA+sinB,
∴sinCcosA+sinCcosB=sin(B+C)+sin(A+C)=sinBcosC+cosBsinC+sinAcosC+cosAsinC,
∴sinBcosC+sinAcosC=0,sinB+sinA≠0,
∴cosC=0,C∈(0,π).
∴![]() .
.
故选:B.


科目:高中数学 来源: 题型:
【题目】2018年12月1日,贵阳市地铁一号线全线开通,在一定程度上缓解了出行的拥堵状况.为了了解市民对地铁一号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图:
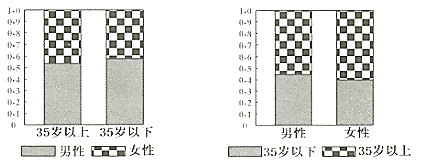
根据图中(![]() 岁以上含
岁以上含![]() 岁)的信息,下列结论中不一定正确的是( )
岁)的信息,下列结论中不一定正确的是( )
A. 样本中男性比女性更关注地铁一号线全线开通
B. 样本中多数女性是![]() 岁以上
岁以上
C. ![]() 岁以下的男性人数比
岁以下的男性人数比![]() 岁以上的女性人数多
岁以上的女性人数多
D. 样本中![]() 岁以上的人对地铁一号线的开通关注度更高
岁以上的人对地铁一号线的开通关注度更高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 相互平行”的充分不必条件
相互平行”的充分不必条件
B.“直线![]() 垂直平面
垂直平面![]() 内无数条直线”是“直线
内无数条直线”是“直线![]() 垂直于平面
垂直于平面![]() ”的充分条件
”的充分条件
C.已知![]() 、
、![]() 、
、![]() 为非零向量,则“
为非零向量,则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D.![]() :存在
:存在![]() ,
,![]() .则
.则![]() :任意
:任意![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是直线
是直线![]() 上任意一点,过
上任意一点,过![]() 作圆
作圆![]() 切线,切点为
切线,切点为![]() ,
,![]() ,求四边形
,求四边形![]() (点
(点![]() 为圆
为圆![]() 的圆心)面积的最小值.
的圆心)面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列,又称黄金分割数列.因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、…..,在数学上,斐波那契数列以如下被递推的方法定义:![]() ,
,![]() ,
,![]() .这种递推方法适合研究生活中很多问题.比如:一六八中学食堂一楼到二楼有15个台阶,某同学一步可以跨一个或者两个台阶,则他到二楼就餐有( )种上楼方法.
.这种递推方法适合研究生活中很多问题.比如:一六八中学食堂一楼到二楼有15个台阶,某同学一步可以跨一个或者两个台阶,则他到二楼就餐有( )种上楼方法.
A.377B.610C.987D.1597
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“沉鱼、落雁、闭月、羞花”是由精彩故事组成的历史典故.“沉鱼”,讲的是西施浣纱的故事;“落雁”,指的就是昭君出塞的故事;“闭月”,是述说貂蝉拜月的故事;“羞花”,谈的是杨贵妃醉酒观花时的故事.她们分别是中国古代的四大美女.某艺术团要以四大美女为主题排演一部舞蹈剧,已知乙扮演杨贵妃,甲、丙、丁三人抽签决定扮演的对象,则甲不扮演貂蝉且丙扮演昭君的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B为函数![]() 图象上相异两点,且A,B的横坐标之积为常数
图象上相异两点,且A,B的横坐标之积为常数![]() ,若
,若![]() 在A,B两点处的切线存在交点,则称这个交点为函数
在A,B两点处的切线存在交点,则称这个交点为函数![]() 的“
的“![]() 点”。
点”。
(1)求函数![]() 的“
的“![]() 点”的纵坐标的取值范围;
点”的纵坐标的取值范围;
(2)判断函数![]() 的
的![]() 点”在哪个象限,并说明理由.
点”在哪个象限,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com