
【题目】下列命题中正确的是( )
A.“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 相互平行”的充分不必条件
相互平行”的充分不必条件
B.“直线![]() 垂直平面
垂直平面![]() 内无数条直线”是“直线
内无数条直线”是“直线![]() 垂直于平面
垂直于平面![]() ”的充分条件
”的充分条件
C.已知![]() 、
、![]() 、
、![]() 为非零向量,则“
为非零向量,则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D.![]() :存在
:存在![]() ,
,![]() .则
.则![]() :任意
:任意![]() ,
,![]()
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,证明:
,证明:![]() 为定值;
为定值;
(2)若![]() 是椭圆
是椭圆![]() 上的两个动点(都不与
上的两个动点(都不与![]() 重合),直线
重合),直线![]() 的斜率互为相反数,求直线
的斜率互为相反数,求直线![]() 的斜率(结果用
的斜率(结果用![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,证明:
,证明:![]() 为定值;
为定值;
(2)若![]() 是椭圆
是椭圆![]() 上的两个动点(都不与
上的两个动点(都不与![]() 重合),直线
重合),直线![]() 的斜率互为相反数,求直线
的斜率互为相反数,求直线![]() 的斜率(结果用
的斜率(结果用![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 是等边三角形,四边形ABCD是矩形,
是等边三角形,四边形ABCD是矩形,![]() ,F为棱PA上一点,且
,F为棱PA上一点,且![]() ,M为AD的中点,四棱锥
,M为AD的中点,四棱锥![]() 的体积为
的体积为![]() .
.
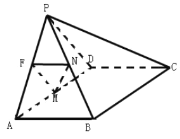
(1)若![]() ,N是PB的中点,求证:平面
,N是PB的中点,求证:平面![]() 平面PCD;
平面PCD;
(2)是否存在![]() ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以ABCDEF为顶点的五面体中,底面ABCD为菱形,∠ABC=120°,AB=AE=ED=2EF,EF![]() AB,点G为CD中点,平面EAD⊥平面ABCD.
AB,点G为CD中点,平面EAD⊥平面ABCD.
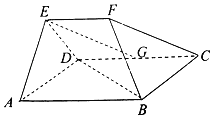
(1)证明:BD⊥EG;
(2)若三棱锥![]() ,求菱形ABCD的边长.
,求菱形ABCD的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】驾驶员“科目一”考试,又称科目一理论考试、驾驶员理论考试,是机动车驾驶证考核的一部分.根据《机动车驾驶证申领和使用规定》,考试内容包括驾车理论基础、道路安全法律法规、地方性法规等相关知识.考试形式为上机考试100道题,90分及以上过关.考试规则是:若上午第一次考试未通过,当场可以立刻补考一次;如果补考还没过,那么出了考场缴费后,下午可以再考,若还未通过可再补考一次.已知小王每一次通过考试的概率均为0.5,且每一场考试与补考是否通过相互独立,则当天小王通过“科目一”考试的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com