
【题目】设抛物线![]() 的焦点为F,准线为
的焦点为F,准线为![]() ,直线l与C交于A,B两点,线段AB中点M的横坐标为2.
,直线l与C交于A,B两点,线段AB中点M的横坐标为2.
(1)求C的方程;
(2)若l经过F,求l的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据抛物线的准线方程,即可求得抛物线的标准方程.
(2)作![]() 垂直准线交于
垂直准线交于![]() ,作
,作![]() 垂直准线交于
垂直准线交于![]() ,交
,交![]() 轴于
轴于![]() ,作
,作![]() 垂直准线交于
垂直准线交于![]() .当直线斜率不存在时,不合题意,当斜率存在时,设出直线方程,联立抛物线,化简后由韦达定理并结合中点的横坐标,即可确定斜率,进而求得直线方程.
.当直线斜率不存在时,不合题意,当斜率存在时,设出直线方程,联立抛物线,化简后由韦达定理并结合中点的横坐标,即可确定斜率,进而求得直线方程.
(1)抛物线![]() 的准线为
的准线为![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以抛物线![]() .
.
(2)作![]() 垂直准线交于
垂直准线交于![]() ,作
,作![]() 垂直准线交于
垂直准线交于![]() ,交
,交![]() 轴于
轴于![]() ,作
,作![]() 垂直准线交于
垂直准线交于![]() ,几何关系如下图所示:
,几何关系如下图所示:

因为线段AB中点M的横坐标为2.
则![]() ,
,
由梯形中位线可知![]()
由抛物线定义可知![]()
直线![]() 经过F,当斜率不存在时
经过F,当斜率不存在时![]() ,不合题意,
,不合题意,
所以直线![]() 斜率一定存在,
斜率一定存在,
抛物线![]() ,则焦点
,则焦点![]() .
.
设直线![]() 的方程为
的方程为![]() ,
,
联立抛物线 ,化简可得
,化简可得![]() ,
,
则![]() ,
,
解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】为了研究玉米品种对产量的 ,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
高茎 | 矮茎 | 总计 | |
圆粒 | 11 | 19 | 30 |
皱粒 | 13 | 7 | 20 |
总计 | 24 | 26 | 50 |
(1)现采用分层抽样的方法,从该样本所含的圆粒玉米中取出6株玉米,再从这6株玉米中随机选出2株,求这2株之中既有高茎玉米又有矮茎玉米的概率;
(2)根据玉米生长情况作出统计,是否有95%的把握认为玉米的圆粒与玉米的高茎有关?
附: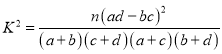
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校学生课外时间的分配情况,拟采用分层抽样的方法从该校的高一、高二、高三这三个年级中共抽取5个班进行调查,已知该校的高一、高二、高三这三个年级分别有18、6、6个班级.
(Ⅰ)求分别从高一、高二、高三这三个年级中抽取的班级个数;
(Ⅱ)若从抽取的5个班级中随机抽取2个班级进行调查结果的对比,求这2个班级中至少有1个班级来自高一年级的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月1日,贵阳市地铁一号线全线开通,在一定程度上缓解了出行的拥堵状况.为了了解市民对地铁一号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图:
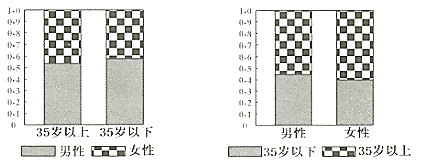
根据图中(![]() 岁以上含
岁以上含![]() 岁)的信息,下列结论中不一定正确的是( )
岁)的信息,下列结论中不一定正确的是( )
A. 样本中男性比女性更关注地铁一号线全线开通
B. 样本中多数女性是![]() 岁以上
岁以上
C. ![]() 岁以下的男性人数比
岁以下的男性人数比![]() 岁以上的女性人数多
岁以上的女性人数多
D. 样本中![]() 岁以上的人对地铁一号线的开通关注度更高
岁以上的人对地铁一号线的开通关注度更高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,又过
两点,又过![]() 两点分别作抛物线的切线,两条切线交于
两点分别作抛物线的切线,两条切线交于![]() 点。
点。
(1)证明:直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为π,它的一个对称中心为(
的最小正周期为π,它的一个对称中心为(![]() ,0)
,0)
(1)求函数y=f(x)图象的对称轴方程;
(2)若方程f(x)=![]() 在(0,π)上的解为x1,x2,求cos(x1-x2)的值.
在(0,π)上的解为x1,x2,求cos(x1-x2)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列
,若去除所有为1的项,依次构成数列![]() ,则此数列的前55项和为( )
,则此数列的前55项和为( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 相互平行”的充分不必条件
相互平行”的充分不必条件
B.“直线![]() 垂直平面
垂直平面![]() 内无数条直线”是“直线
内无数条直线”是“直线![]() 垂直于平面
垂直于平面![]() ”的充分条件
”的充分条件
C.已知![]() 、
、![]() 、
、![]() 为非零向量,则“
为非零向量,则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D.![]() :存在
:存在![]() ,
,![]() .则
.则![]() :任意
:任意![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com