
【题目】设函数![]() (
(![]() ).
).
(1)讨论函数![]() 的单调性;
的单调性;
(2)若关于x的方程![]() 有唯一的实数解,求a的取值范围.
有唯一的实数解,求a的取值范围.
【答案】(1)当![]() 时,
时,![]() 递增区间时
递增区间时![]() ,无递减区间,当
,无递减区间,当![]() 时,
时,![]() 递增区间时
递增区间时![]() ,递减区间时
,递减区间时![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)求出![]() ,对
,对![]() 分类讨论,先考虑
分类讨论,先考虑![]() (或
(或![]() )恒成立
)恒成立![]() 的范围,并以此作为
的范围,并以此作为![]() 的分类标准,若不恒成立,求解
的分类标准,若不恒成立,求解![]() ,即可得出结论;
,即可得出结论;
(2)![]() 有解,即
有解,即![]() ,令
,令![]() ,转化求函数
,转化求函数![]() 只有一个实数解,根据(1)中的结论,即可求解.
只有一个实数解,根据(1)中的结论,即可求解.
(1)![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,
,
综上,当![]() 时,
时,![]() 递增区间时
递增区间时![]() ,无递减区间,
,无递减区间,
当![]() 时,
时,![]() 递增区间时
递增区间时![]() ,递减区间时
,递减区间时![]() ;
;
(2)![]() ,
,
![]()
令![]() ,原方程只有一个解,只需
,原方程只有一个解,只需![]() 只有一个解,
只有一个解,
即求![]() 只有一个零点时,
只有一个零点时,![]() 的取值范围,
的取值范围,
由(1)得当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
且![]() ,函数只有一个零点,原方程只有一个解
,函数只有一个零点,原方程只有一个解![]() ,
,
当![]() 时,由(1)得
时,由(1)得![]() 在
在![]() 出取得极小值,也是最小值,
出取得极小值,也是最小值,
当![]() 时,
时,![]() ,此时函数只有一个零点,
,此时函数只有一个零点,
原方程只有一个解![]() ,
,
当![]() 且
且![]()
递增区间时![]() ,递减区间时
,递减区间时![]() ;
;
![]() ,当
,当![]() ,
,
![]() 有两个零点,
有两个零点,
即原方程有两个解,不合题意,
所以![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】在一项自“一带一路”沿线20国青年参与的评选中“高铁”、“支付宝”、“共享单车”和“网购”被称作中国“新四大发明”,曾以古代“四大发明”推动世界进步的中国,正再次以科技创新向世界展示自己的发展理念.某班假期分为四个社会实践活动小组,分别对“新四大发明”对人们生活的影响进行调查.于开学进行交流报告会.四个小组随机排序,则“支付宝”小组和“网购”小组不相邻的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,证明:
,证明:![]() 为定值;
为定值;
(2)若![]() 是椭圆
是椭圆![]() 上的两个动点(都不与
上的两个动点(都不与![]() 重合),直线
重合),直线![]() 的斜率互为相反数,求直线
的斜率互为相反数,求直线![]() 的斜率(结果用
的斜率(结果用![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 是等边三角形,四边形ABCD是矩形,
是等边三角形,四边形ABCD是矩形,![]() ,F为棱PA上一点,且
,F为棱PA上一点,且![]() ,M为AD的中点,四棱锥
,M为AD的中点,四棱锥![]() 的体积为
的体积为![]() .
.
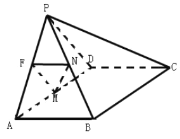
(1)若![]() ,N是PB的中点,求证:平面
,N是PB的中点,求证:平面![]() 平面PCD;
平面PCD;
(2)是否存在![]() ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以ABCDEF为顶点的五面体中,底面ABCD为菱形,∠ABC=120°,AB=AE=ED=2EF,EF![]() AB,点G为CD中点,平面EAD⊥平面ABCD.
AB,点G为CD中点,平面EAD⊥平面ABCD.
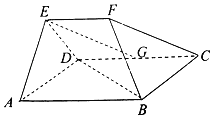
(1)证明:BD⊥EG;
(2)若三棱锥![]() ,求菱形ABCD的边长.
,求菱形ABCD的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长沙某超市计划按月订购一种冰激凌,每天进货量相同,进货成本为每桶5元,售价为每桶7元,未售出的冰激凌以每桶3元的价格当天全部处理完毕.根据往年销售经验,每天的需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于
)有关,如果最高气温不低于![]() ,需求量为600桶;如果最高气温(单位:
,需求量为600桶;如果最高气温(单位:![]() )位于区间
)位于区间![]() ,需求量为400桶;如果最高气温低于
,需求量为400桶;如果最高气温低于![]() ,需求量为200桶.为了确定今年九月份的订购计划,统计了前三年九月份各天的最高气温数据,得下面的频数分布表:
,需求量为200桶.为了确定今年九月份的订购计划,统计了前三年九月份各天的最高气温数据,得下面的频数分布表:
最高气温( |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求九月份这种冰激凌一天的需求量![]() (单位:桶)的分布列;
(单位:桶)的分布列;
(2)设九月份一天销售这种冰激凌的利润为![]() (单位:元),当九月份这种冰激凌一天的进货量
(单位:元),当九月份这种冰激凌一天的进货量![]() (单位:桶)为多少时,
(单位:桶)为多少时,![]() 的均值取得最大值?
的均值取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com