
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)对直线![]() 的斜率是否存在进行分类讨论,利用圆心到直线
的斜率是否存在进行分类讨论,利用圆心到直线![]() 的距离等于2可求得直线
的距离等于2可求得直线![]() 的方程;
的方程;
(2)先通过点到直线的距离及勾股定理可解得直线![]() 的斜率,然后将直线
的斜率,然后将直线![]() 的方程与圆的方程联立,求出线段
的方程与圆的方程联立,求出线段![]() 的中点,作为圆心,并求出所求圆的半径,进而可得出所求圆的方程.
的中点,作为圆心,并求出所求圆的半径,进而可得出所求圆的方程.
(1)由题意知,圆![]() 的标准方程为
的标准方程为![]() ,
,![]() 圆心
圆心![]() ,半径
,半径![]() ,
,
①当直线![]() 的斜率
的斜率![]() 存在时,设直线的方程为
存在时,设直线的方程为![]() ,即
,即![]() ,
,
则圆心到直线![]() 的距离为
的距离为![]() ,
,![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() ;
;
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
此时圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,符合题意.
,符合题意.
综上所述,直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)依题意可设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
则圆心![]() 到直线
到直线![]() 的距离
的距离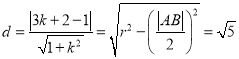 ,
,
![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,
,![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() 即
即![]() ,
,
设点![]() 、
、![]() ,联立直线
,联立直线![]() 与圆
与圆![]() 的方程得
的方程得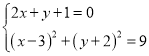 ,
,
消去![]() 得
得![]() ,
,![]() ,
,
则线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,把
,把![]() 代入直线
代入直线![]() 中得
中得![]() ,
,
所以,线段![]() 的中点的坐标为
的中点的坐标为![]() ,
,
由题意知,所求圆的半径为:![]() ,
,
![]() 以线段
以线段![]() 为直径的圆的方程为:
为直径的圆的方程为:![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
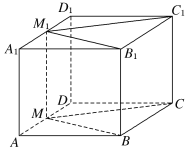
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.
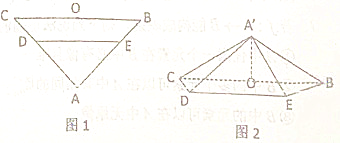
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数茎叶图如下:
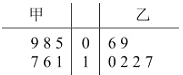
(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意![]() 都有
都有![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() ,给出如下命题:
,给出如下命题:
①![]() ;
;
②直线![]() 是函数
是函数![]() 的图象的一条对称轴;
的图象的一条对称轴;
③函数![]() 在
在![]() 上为增函数;
上为增函数;
④函数![]() 在
在![]() 上有四个零点.
上有四个零点.
其中所有正确命题的序号为( )
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某地某年月平均气温(华氏度):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
以月份为x轴(![]() 月份
月份![]() ),以平均气温为y轴.
),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com