
| A. | p是假命题 | B. | ¬q是真命题 | C. | p∨q是假命题 | D. | p∨q是真命题 |
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 存在x0∈R,使得${x_0}^2+1>0$ | B. | 存在x0∈R,使得${x_0}^2+1≤0$ | ||
| C. | 存在x0∈R,使得${x_0}^2+1<0$ | D. | 存在x0∈R,使得${x_0}^2+1≥0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
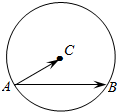 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不是奇函数也不是偶函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是偶函数 | D. | 是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数
我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com