
| A. | 既不是奇函数也不是偶函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是偶函数 | D. | 是奇函数 |
分析 由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,函数f(x)=(x$\overrightarrow{a}$+$\overrightarrow{b}$)2 =x2+1,由此可得函数的奇偶性.
解答 解:由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,
∴函数f(x)=(x$\overrightarrow{a}$+$\overrightarrow{b}$)2 =x2+2$\overrightarrow{a}$•$\overrightarrow{b}$x+1=x2+1,
显然,函数f(x)为偶函数,
故选C.
点评 本题主要考查两个向量垂直的性质,函数的奇偶性的判断,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题 | B. | ¬q是真命题 | C. | p∨q是假命题 | D. | p∨q是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
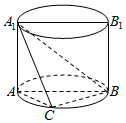 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com