
分析 根据向量的夹角公式,以及向量的垂直,向量模计算即可.
解答 解:设$(\vec a+\vec b)$与$\vec b$的夹角为θ,
∵$|\vec a+\vec b|=|\vec a-\vec b|$,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$-$\overrightarrow{b}$|2,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∵$(\vec a+\vec b)⊥(\vec a-\vec b)$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,
∴$|\overrightarrow{a}|$=$|\overrightarrow{b}|$,
∴$(\vec a+\vec b)$•$\vec b$=${\overrightarrow{b}}^{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{b}$|,
∴cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}+\overrightarrow{b}|•|\overrightarrow{b}|}$=$\frac{\sqrt{2}}{2}$,
∵0≤θ≤180°,
∴θ=45°,
故答案为:45°.
点评 本题考查了向量的数量积的运算以及向量的模的计算以及向量垂直的条件,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
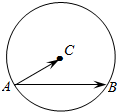 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不是奇函数也不是偶函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是偶函数 | D. | 是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com