
分析 由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2ωx-$\frac{π}{6}$)+$\frac{1}{2}$,结合ω>0,由周期公式即可解得ω的值,从而解得f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$,由正弦函数的单调性可得f(x)在$[\frac{π}{4},\;\frac{π}{2}]$上的最小值.
解答 解:∵f(x)=sin2ωx+$\sqrt{3}$sinωxsin(ωx+$\frac{π}{2}$)
=$\frac{1-cos2ωx}{2}$+$\sqrt{3}$sinωxcosωx
=sin(2ωx-$\frac{π}{6}$)+$\frac{1}{2}$,
∴由ω>0,π=$\frac{2π}{2ω}$,可解得:ω=1.
∴可得f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$,
∵x∈$[\frac{π}{4},\;\frac{π}{2}]$,可得:2x-$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],
∴f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$∈[1,$\frac{3}{2}$],
∴f(x)在$[\frac{π}{4},\;\frac{π}{2}]$上的最小值是1.
故答案为:1,1;
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
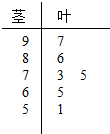 北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩.
北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-5x+1≤0 | B. | ?x∈R,x2-5x+1≤0 | C. | ?x∈R,x2-5x+1<0 | D. | ?x∈R,x2-5x+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
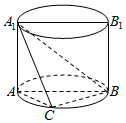 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com