
分析 (1)化简F(x)=2loga(x+1)+loga$\frac{1}{1-x}$,由$\left\{\begin{array}{l}{x+1>0}\\{1-x>0}\end{array}\right.$确定函数F(x)的定义域,从而在定义域内确定方程F(x)=0的解即可.
(2)y=x+1与y=$\frac{1}{1-x}$在区间[0,1)上均为增函数,从而由复合函数单调性确定函数的单调性,从而分类讨论即可.
解答 解:(1)∵f(x)=loga(x+1),g(x)=loga$\frac{1}{1-x}$,
∴F(x)=2f(x)+g(x)
=2loga(x+1)+loga$\frac{1}{1-x}$,
由$\left\{\begin{array}{l}{x+1>0}\\{1-x>0}\end{array}\right.$解得,
函数F(x)的定义域为(-1,1),
令F(x)=0得,
2loga(x+1)+loga$\frac{1}{1-x}$=0,
故2loga(x+1)=loga(1-x),
故(x+1)2=1-x,
故x2+3x=0,
解得,x=0或x=-3,
故F(x)的零点为0;
(2)∵y=x+1与y=$\frac{1}{1-x}$在区间[0,1)上均为增函数,
∴根据复合函数单调性知,
①当a>1时,函数F(x)=2f(x)+g(x)在区间[0,1)上是增函数,
②当0<a<1时,函数F(x)=2f(x)+g(x)在区间[0,1)上是减函数;
∴关于x的方程F(x)=2m2-3m-5在区间[0,1)最多有一解,
∵关于x的方程F(x)=2m2-3m-5在区间[0,1)内仅有一解,
①当a>1时,函数F(x)在区间[0,1)上是增函数且F(0)=0,
$\underset{lim}{x→1}$F(x)=+∞,
故只需使2m2-3m-5≥0,
解得,m≤-1或m≥$\frac{5}{2}$;
②当0<a<1时,函数F(x)在区间[0,1)上是减函数且F(0)=0,
$\underset{lim}{x→1}$F(x)=-∞,
故只需使2m2-3m-5≤0,
解得,-1≤m≤$\frac{5}{2}$;
综上所述,当a>1时,m≤-1或m≥$\frac{5}{2}$;
当0<a<1时,-1≤m≤$\frac{5}{2}$.
点评 本题考查了函数的零点与方程的根的关系应用及分类讨论的思想应用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{29}$ | B. | $\frac{16}{27}$ | C. | $\frac{11}{13}$ | D. | $\frac{13}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
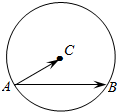 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不是奇函数也不是偶函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是偶函数 | D. | 是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数
我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+2=0 | B. | 3x-y+1=0 | ||
| C. | 8x-y-4=0 | D. | 2x-y+2=0或8x-y-4=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com