
分析 由已知求出椭圆的焦点,准线方程,设△MNF2为等腰直角三角形,且MN=NF2,MN⊥NF2,设N到下准线的距离为m,M到上准线的距离为n,由椭圆的第二定义,利用合分比性质,以及勾股定理得到关于a的方程,解方程可得a,再由离心率公式求得答案.
解答 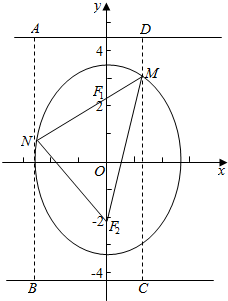 解:由椭圆Γ:$\frac{{x}^{2}}{{a}^{2}-4}$+$\frac{{y}^{2}}{{a}^{2}}$=1(a>2),
解:由椭圆Γ:$\frac{{x}^{2}}{{a}^{2}-4}$+$\frac{{y}^{2}}{{a}^{2}}$=1(a>2),
得c2=a2-(a2-4)=4,∴c=2,
则椭圆的上、下焦点分别为F1(0,2),F2(0,-2),
离心率e=$\frac{2}{a}$,准线方程为y=±$\frac{{a}^{2}}{2}$,
如图△MNF2为等腰直角三角形,且MN=NF2,MN⊥NF2,
设N到下准线的距离为m,M到上准线的距离为n,
由椭圆的定义可得,e=$\frac{N{F}_{2}}{m}$=$\frac{N{F}_{1}}{{a}^{2}-m}$=$\frac{M{F}_{1}}{n}=\frac{M{F}_{2}}{{a}^{2}-n}$,
即有$\frac{N{F}_{2}}{m}=\frac{MN}{{a}^{2}-m+n}=\frac{M{F}_{2}}{{a}^{2}-n}$=$\frac{\sqrt{2}MN}{{a}^{2}-n}=\frac{MN}{m}$,
则2m-n=a2,($\sqrt{2}$+1)n-$\sqrt{2}$m=(1-$\sqrt{2}$)a2,
解得:m=(2-$\sqrt{2}$)a2,
又NF12+NF22=F1F22=16,
即有($\frac{2}{a}$(a2-m))2+($\frac{2}{a}$•m))2=16,
代入m=(2-$\sqrt{2}$)a2,解方程可得a=$\frac{2}{3}(\sqrt{6}+\sqrt{3})$,
即有${e}^{2}=(\frac{c}{a})^{2}=(\frac{2}{\frac{2}{3}(\sqrt{6}+\sqrt{3})})^{2}=(\sqrt{6}-\sqrt{3})^{2}$=$9-3\sqrt{2}$.
故答案为:$9-3\sqrt{2}$.
点评 本题考查椭圆的定义、方程和性质,考查比例的性质和勾股定理的运用,考查灵活变形及运算能力,属难题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 既不是奇函数也不是偶函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是偶函数 | D. | 是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com