Question

17．已知函数f（x）=ax+lnx（a∈R），g（x）=$\frac{{x}^{2}}{x-lnx}$．
（1）当a=1时，求f（x）的单调增区间；
（2）若h（x）=f（x）-g（x）恰有三个不同的零点x₁，x₂，x₃（x₁＜x₂＜x₃）．
①求实数a的取值范围；
②求证：（1-$\frac{ln{x}_{1}}{{x}_{1}}$）²（1-$\frac{ln{x}_{2}}{{x}_{2}}$）（1-$\frac{ln{x}_{3}}{{x}_{3}}$）=1．

Answer 1

分析 （1）把a=1代入函数解析式，求导后得到其单调区间，注意到函数的定义域．
（2）①先分离参数得到$a=\frac{x}{x-lnx}-\frac{lnx}{x}$，令h（x）=$\frac{x}{x-lnx}-\frac{lnx}{x}$．求导后得其极值点，求得函数极值，则使h（x）恰有三个零点的实数a的范围可求．
②由a=$\frac{x}{x-lnx}-\frac{lnx}{x}$=$\frac{1}{1-\frac{lnx}{x}}-\frac{lnx}{x}$，再令$μ=\frac{lnx}{x}$，转化为关于μ的方程后由根与系数关系得到μ₁+μ₂=1-a＜0，μ₁μ₂=1-a＜0，再结合着$μ=\frac{lnx}{x}$的图象可得到$（1-\frac{ln{x}_{1}}{{x}_{1}}）^{2}（1-\frac{ln{x}_{2}}{{x}_{2}}）（1-\frac{ln{x}_{3}}{{x}_{3}}）$=1

解答 （1）当a=1时，$f′（x）=1+\frac{1}{x}$＞0（x＞0），
∴f（x）的单调增区间为（0，+∞）．
（2）①令$h（x）=ax+lnx-\frac{{x}^{2}}{x-lnx}$=0，
分离参数得$a=\frac{x}{x-lnx}-\frac{lnx}{x}$，
令h（x）=$\frac{x}{x-lnx}-\frac{lnx}{x}$，
由h′（x）=$\frac{1-lnx}{（x-lnx）^{2}}-\frac{1-lnx}{{x}^{2}}$=$\frac{lnx（1-lnx）（2x-lnx）}{{x}^{2}（x-lnx）^{2}}$=0，得x=1或x=e．
列表知，当x∈（0，1）时，h′（x）＜0；当x∈（1，e）时，h′（x）＞0；当x∈（e，+∞）时，h′（x）＜0．
即h（x）在（0，1），（e，+∞）上为减函数，在（1，e）上为增函数．
而当x→0，h（x）→+∞，当x→+∞，h（x）→1，又h（1）=1，h（e）=$1+\frac{1}{e（e-1）}$；
结合函数的单调性可得，实数a的取值范围为（1，$1+\frac{1}{e（e-1）}$）．
②由①可知，0＜x₁＜1＜x₂＜e＜x₃，
a=$\frac{x}{x-lnx}-\frac{lnx}{x}$=$\frac{1}{1-\frac{lnx}{x}}-\frac{lnx}{x}$，令$μ=\frac{lnx}{x}$，
则a=$\frac{1}{1-μ}-μ$，即μ²+（a-1）μ+1-a=0，
μ₁+μ₂=1-a＜0，μ₁μ₂=1-a＜0，
对于$μ=\frac{lnx}{x}$，$μ′=\frac{1-lnx}{{x}^{2}}$
则当0＜x＜e时，μ′＞0；当x＞e时，μ′＜0．而当x＞e时，μ恒大于0．
画其简图，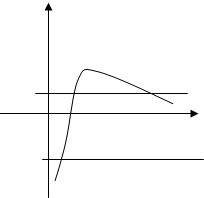
不妨设μ₁＜μ₂，则${μ}_{1}=\frac{ln{x}_{1}}{{x}_{1}}，{μ}_{2}=\frac{ln{x}_{2}}{{x}_{2}}=\frac{ln{x}_{3}}{{x}_{3}}$，
∴$（1-\frac{ln{x}_{1}}{{x}_{1}}）^{2}（1-\frac{ln{x}_{2}}{{x}_{2}}）（1-\frac{ln{x}_{3}}{{x}_{3}}）$=$（1-{μ}_{1}）^{2}（1-{μ}_{2}）（1-{μ}_{2}）$=$[（1-{μ}_{1}）（1-{μ}_{2}）]^{2}$
=$[1-（{μ}_{1}+{μ}_{2}）+{μ}_{1}{μ}_{2}]^{2}$
=[1-（1-a）+（1-a）]²=1

点评 本题考察了利用函数研究函数单调性，极值等性质，训练了函数零点的判断方法，运用了分离变量法，换元法，函数构造法等数学转化思想方法，综合性强属于压轴题范畴．