
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由x1-x2)[f(x1)-f(x2)]>0,等价为函数f(x)为增函数,利用导数或函数单调性的性质判断函数的单调性即可.
解答 解:若函数f(x)对任意两个不相等的实数x1,x2,都有(x1-x2)[f(x1)-f(x2)]>0,
则等价为函数f(x)为增函数,
则①y=-x3+x+1;
则y′=-3x2+1,由f′(x)>0得-$\frac{\sqrt{3}}{3}$<x<$\frac{\sqrt{3}}{3}$,则函数的单调递增区间为不是(-∞,+∞),不满足条件.
②y=3x-2(sinx-cosx);
则y′=3-2$\sqrt{2}$sin(x+$\frac{π}{4}$)>0恒成立,即函数在(-∞,+∞)上为增函数满足条件.
③y=ex+1在(-∞,+∞)为增函数,满足条件;
④$f(x)=\left\{\begin{array}{l}ln|x|{\;}_{\;}^{\;}x≠0\\ 0{\;}_{\;}^{\;}{\;}_{\;}^{\;}x=0\end{array}\right.$为偶函数,在(-∞,+∞)不是单调递增函数,不满足条件.
故“H函数”的个数为2个,
故选:B.
点评 本题主要考查与函数有关的新定义,弄懂题意,将条件转化为函数的单调递增函数是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα<tanα<cosα | B. | tanα<sinα<cosα | C. | cosα<sinα<tanα | D. | sinα<cosα<tanα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
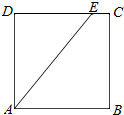 如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.
如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份x年 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com