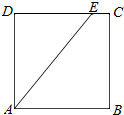
如图.在边长为2的正方形ABCD中.E为正方形边上的动点.现将△ADE所在平面沿AE折起.使点D在平面ABC上的射影H在直线AE上.当E从点D运动到C.再从C运动到B.则点H所形成轨迹的长度为π．题目和参考答案——青夏教育精英家教网—

18．

如图，在边长为2的正方形ABCD中，E为正方形边上的动点，现将△ADE所在平面沿AE折起，使点D在平面ABC上的射影H在直线AE上，当E从点D运动到C，再从C运动到B，则点H所形成轨迹的长度为π．

分析根据图形的翻折过程中变与不变的量和位置关系知，在平面AED内过点D作DH⊥AE，H为垂足，由翻折的特征知，连接D'H，则∠D'HA=90°，当E从点D运动到C，再从C运动到B，故H点的轨迹是以AD'为直径的半圆弧，根据长方形的边长得到圆的半径，利用弧长公式求出轨迹长度．

解答解：由题意，在平面AED内过点D作DH⊥AE，H为垂足，由翻折的特征知，连接D'H．
则∠D'HA=90°，
当E从点D运动到C，再从C运动到B，故H点的轨迹是以AD'为直径的半圆弧，
根据边长为2的正方形ABCD知圆半径是1，
所以其所对的弧长为π，
故答案为：π

点评本题考查与二面角有关的立体几何综合题目，解题的关键是由题意得出点H的轨迹是圆上的一段弧，翻折问题中要注意位置关系与长度等数量的变与不变．本题是一个中档题目．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

8．

如图所示，AB为半圆ACB的水平直径，C为圆上的最低点，一小球从A点以速度v₀被水平抛出后恰好落在C点，设重力加速度为g，不计空气阻力，求圆的半径．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．已知点O为△ABC的外心，且AC=4，AB=2，则$\overrightarrow{AO}$•（$\overrightarrow{AC}$-$\overrightarrow{AB}$）=6．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．如果对定义在R上的函数f（x）对任意两个不相等的实数x₁，x₂，都有（x₁-x₂）[f（x₁）-f（x₂）]＞0，则称函数f（x）为“H函数”．给出下列函数①y=-x³+x+1；②y=3x-2（sinx-cosx）；③y=e^x+1；④$f（x）=\left\{\begin{array}{l}ln|x|{\;}_{\;}^{\;}x≠0\\ 0{\;}_{\;}^{\;}{\;}_{\;}^{\;}x=0\end{array}\right.$．其中“H函数”的个数为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．已知实数u，v满足u＞|v|，2u=3（u²-v²），则3u+v的取值范围是[$\frac{3+2\sqrt{2}}{3}，+∞$）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．设f（x）=e^x-e^-x-ax（a∈R）．
（Ⅰ）若f（x）在R上是单调函数，求实数a的取值范围；
（Ⅱ）证明：当x∈R时，e^x+e^-x≥x²+2；
（Ⅲ）证明：当x≥0时，对任意n∈N⁺，e^x+e^-x≥2+2[$\frac{{x}^{2}}{2!}$+$\frac{{x}^{4}}{4!}$+…+$\frac{{x}^{2n}}{（2n）!}$]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．已知椭圆C的中心在坐标原点O，左、右焦点分别为F₁、F₂，点A时椭圆C上任一点，且|AF₁|•|AF₂|的最大值为3，以椭圆C的右焦点为圆心，焦距为直径的圆与直线l₁：x+$\sqrt{3}$y+1=0相切．
（1）求椭圆C的标准方程；
（2）不过原点的直线l₂与椭圆C交于P（x₁，y₁），Q（x₂，y₂）两个不同点，以OP，OQ为邻边作?OQNP，当?OQNP的面积为$\sqrt{6}$时，证明：|ON|²+|PQ|²为定值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．若$tanα=\frac{1}{2}$，则$\frac{2sinα+cosα}{4sinα-cosα}$=2．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．若a＞0，b＜0，则下列不等式中正确的是（　　）

A．

a＜b

B．

$\frac{1}{a}$＜$\frac{1}{b}$

C．

a²＞b²