
分析 根据向量射影定理,数量积的运算性质即可得出.
解答 解:O为△ABC的外心,且AC=4,AB=2,
∴$\overrightarrow{AO}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{AO}$$•\overrightarrow{AC}$-$\overrightarrow{AO}$•$\overrightarrow{AB}$=|$\overrightarrow{AO}$|•|$\overrightarrow{AC}$|cos120°-|$\overrightarrow{AO}$|•|$\overrightarrow{AB}$|cos120°=$\frac{1}{2}$|$\overrightarrow{AC}$|2-$\frac{1}{2}$|$\overrightarrow{AB}$|2=$\frac{1}{2}$×16-$\frac{1}{2}$×4=6,
故答案为:6.
点评 本题主要考查向量数量积的几何意义.要会巧妙的转化问题.属中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
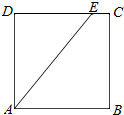 如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.
如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com