
分析 (1)通过记等差数列{an}的公差为d,利用a1=1将a3、a4、a11用d表示出来,进而利用a3,a4+$\frac{5}{2}$,a11成等比数列得出关于d的方程,计算可知公差d=$\frac{3}{2}$,进而计算可得结论;
(2)通过(1)可知a2n=3n-$\frac{1}{2}$、a2n+1-a2n-1=3,利用Tn=(a3-a1)a2+(a5-a3)a4+…+(a2n+1-a2n-1)a2n,分组计算即得结论.
解答 解:(1)记等差数列{an}的公差为d,由a1=1可知,
a3=1+2d,a4+$\frac{5}{2}$=1+3d+$\frac{5}{2}$=$\frac{7}{2}$+3d,a11=1+10d,
又∵a3,a4+$\frac{5}{2}$,a11成等比数列,
∴$(\frac{7}{2}+3d)^{2}$=(1+2d)(1+10d),
整理得:11d2-9d-$\frac{45}{4}$=0,
解得:d=$\frac{3}{2}$或d=-$\frac{15}{22}$(舍),
∴数列{an}的是首项为1、公差为$\frac{3}{2}$的等差数列,
故其通项公式an=1+$\frac{3}{2}$(n-1)=$\frac{3}{2}$n-$\frac{1}{2}$;
(2)由(1)可知an=$\frac{3}{2}$n-$\frac{1}{2}$,a2n=3n-$\frac{1}{2}$,a2n+1-a2n-1=3,
∴Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1
=a1a2-a2a3+a3a4-a4a5+…+a2n-1a2n-a2na2n+1
=(a3-a1)a2+(a5-a3)a4+…+(a2n+1-a2n-1)a2n
=3(a2+a4+…+a2n)
=3(a2+a4+…+a2n)
=3•$\frac{n(3-\frac{1}{2}+3n-\frac{1}{2})}{2}$
=$\frac{9}{2}$n2+3n.
点评 本题考查数列的通项及前n项和,考查分组法求和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
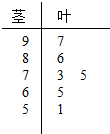 北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩.
北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
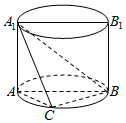 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.
一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB为半圆ACB的水平直径,C为圆上的最低点,一小球从A点以速度v0被水平抛出后恰好落在C点,设重力加速度为g,不计空气阻力,求圆的半径.
如图所示,AB为半圆ACB的水平直径,C为圆上的最低点,一小球从A点以速度v0被水平抛出后恰好落在C点,设重力加速度为g,不计空气阻力,求圆的半径.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com