
 一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.
一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.分析 (1)先根据h的最大和最小值求得A和B,利用周期求得ω,当t=0时,h=0,进而求得φ的值,则函数的表达式可得;
(2)令最大值为6,即h=4sin($\frac{2π}{15}$t-$\frac{π}{6}$)+2=6,可求得时间.
解答 解:(1)依题意可知h的最大值为6,最小为-2,
∴$\left\{\begin{array}{l}{A+B=6}\\{-A+B=-2}\end{array}\right.$,∴A=4,B=2;
∵水轮每秒钟内所转过的角为$\frac{4×2π}{60}$=$\frac{2π}{15}$,得h=4sin($\frac{2π}{15}$t+φ)+2,
当t=0时,h=0,得sinφ=-$\frac{1}{2}$,即φ=-$\frac{π}{6}$,故所求的函数关系式为h=4sin($\frac{2π}{15}$t-$\frac{π}{6}$)+2
(2)令h=4sin($\frac{2π}{15}$t-$\frac{π}{6}$)+2=6,得sin($\frac{2π}{15}$t-$\frac{π}{6}$)=1,
取$\frac{2π}{15}$t-$\frac{π}{6}$=$\frac{π}{2}$,得t=5,
故点P第一次到达最高点大约需要5s.
点评 本题主要考查了在实际问题中建立三角函数模型的问题.考查了运用三角函数的最值,周期等问题确定函数的解析式.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-x-2≤0 | B. | ?x∈R,x2-x-2<0 | C. | ?x∈R,x2-x-2≤0 | D. | ?x∈R,x2-x-2<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
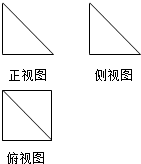 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | ($\frac{1}{2}$,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com