练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知向量$\overrightarrow{AB}$=（1，-4），向量$\overrightarrow{BC}$=（3，1），则|$\overrightarrow{AC}$|=5．

    分析 根据题意，由向量的加法运算法则可得向量$\overrightarrow{AC}$的坐标，进而由向量的模的计算公式计算可得答案．

    解答 解：根据题意，向量$\overrightarrow{AB}$=（1，-4），向量$\overrightarrow{BC}$=（3，1），
    $\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=（4，-3），
    则|$\overrightarrow{AC}$|=$\sqrt{{4}^{2}+（-3）^{2}}$=5，
    故答案为：5．

    点评 本题考查向量的坐标运算，涉及向量模的计算；关键是正确求出向量$\overrightarrow{AC}$的坐标．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．已知命题p：?m∈R，$\frac{1}{{{m^2}+m-6}}＞0$，则命题p的否定形式是$?m∈R，\frac{1}{{{m^2}+m-6}}＜0$或m2+m-6=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．命题“?x∈R，x2-5x+1＞0”的否定为（　　）
    A．?x∈R，x2-5x+1≤0B．?x∈R，x2-5x+1≤0C．?x∈R，x2-5x+1＜0D．?x∈R，x2-5x+1＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

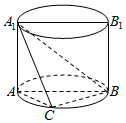    10．如图，AA1B1B是圆柱的轴截面，C是底面圆周上异于A，B的一点，AA1=AB=2．
    （1）求证：平面AA1C⊥平面BA1C；
    （2）若AC=BC，求几何体A1-ABC的体积V．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

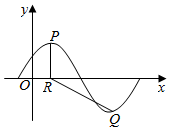    17．如图所示为f（x）=Asin（$\frac{π}{6}$x+φ）（A＞0，0＜φ＜$\frac{π}{2}$）的部分图象，P，Q分别为f（x）图象的最高点和最低点，点P坐标为（2，A），PR⊥x轴于R，若∠PRQ=$\frac{2π}{3}$．则A及φ的值分别是（　　）
    A．$\sqrt{3}$，$\frac{π}{6}$B．$\sqrt{3}$，$\frac{π}{3}$C．2$\sqrt{3}$，$\frac{π}{6}$D．2$\sqrt{3}$，$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知数列{an}满足：a0=0，a1=1，且a2n=an，a2n+1=an+1（n∈N*），则a2013=8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．一半径为4m的水轮，如图所示水轮圆心O距离水面2m，己知水轮每分钟转动4圈，如果当水轮上P点从水中浮现时（图中P0）点开始计算时间．
    （1）求P点相对于水面的高度h（m）与时间t（s）之间的函数关系式：
    （2）P点第一次达到最高点约要多长时间？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设f（x）=3x+3-x，则f（x）是（　　）
    A．偶函数B．奇函数
    C．非奇非偶函数D．既是奇函数又是偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在正项等比数列{an}中，若1og2（a1a2a3…a9）=18，且a2，a4是方程x2+mx+4=0的两根，则数列{an}的通项公式为（　　）
    A．2${\;}^{-\frac{n-3}{2}}$B．2${\;}^{\frac{n-3}{2}}$C．2${\;}^{\frac{n-1}{2}}$D．2${\;}^{\frac{n}{2}}$

    查看答案和解析>>

    同步练习册答案