
分析 (1)求出函数f(x)的导数,由g(x)为奇函数,可得b=-6,c=0;
(2)求出f(x)的导数,代入x=2,计算即可得到所求和;
(3)求得切线的斜率和切点,由点斜式方程,即可得到所求切线的方程.
解答 解:(1)函数f(x)=2x3-bx2+cx的导数为f′(x)=6x2-2bx+c,
函数g(x)=f(x)-f′(x)=2x3-(b+6)x2+(c+2b)x-c,
由奇函数的定义,可得g(-x)=-g(x),
即有b+6=0,c=0,解得b=-6,c=0;
(2)f(x)=2x3+6x2的导数为f′(x)=6x2+12x,
即有f(2)+f′(2)=16+24+24+24=88;
(3)f(x)在点(1,f(1))处的切线斜率为6+12=18,
切点为(1,8),
则f(x)在点(1,f(1))处的切线方程为y-8=x-1,
即为x-y+7=0.
点评 本题考查导数的运用:求切线的方程,同时考查奇函数的定义,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-5x+1≤0 | B. | ?x∈R,x2-5x+1≤0 | C. | ?x∈R,x2-5x+1<0 | D. | ?x∈R,x2-5x+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.
一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB为半圆ACB的水平直径,C为圆上的最低点,一小球从A点以速度v0被水平抛出后恰好落在C点,设重力加速度为g,不计空气阻力,求圆的半径.
如图所示,AB为半圆ACB的水平直径,C为圆上的最低点,一小球从A点以速度v0被水平抛出后恰好落在C点,设重力加速度为g,不计空气阻力,求圆的半径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
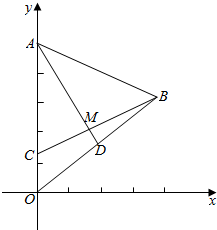 如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC相交于点M,求点M的坐标.
如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC相交于点M,求点M的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2${\;}^{-\frac{n-3}{2}}$ | B. | 2${\;}^{\frac{n-3}{2}}$ | C. | 2${\;}^{\frac{n-1}{2}}$ | D. | 2${\;}^{\frac{n}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com